
논문명: TM-generation model: a template-based method for automatically solving mathematical word problems
논문 링크: https://link.springer.com/article/10.1007/s11227-021-03855-9
요약
- Math Word Problem(이하 MWP) 풀이 태스크의 정확도를 향상시키는 모델 'TM-generation' 제시
- 이를 위해 2개의 challenges 를 정의하고, 각각을 해결하고자 함.

1. filling in missing world knowledge required to solve the given MWP
- 필요성: MWP 를 풀기 위한 상식(world knowledge)을 채울 필요가 있다.
- 예시: '직각삼각형의 두 변의 길이를 알려주고 나머지 한 변의 길이를 구하라는 문제'(MWP)를 풀기 위해선 그 문제에 적혀 있지 않지만 '피타고라스 정리'(world knowledge)를 알아야 한다.
- 방법: 이를 해결하고자, 'ELECTRA'를 사용한다.
2. understanding the implied relationship between numbers and variables.
- 필요성: MWP 속에 존재하는 변수와 숫자 사이의 관계를 이해할 필요가 있다.
- 예시: '마동석은 사탕을 2개, 장첸은 사탕을 1개를 가지고 있다. 이때, 마동석이 장첸에게 사탕을 모두 달라고 한다면 마동석의 사탕은 총 몇개가 될까?' 와 같은 문제가 있다고 가정하자. 이때, 우리는 머리 속으로 자연스럽게 3개임을 읽으면서 계산할 수 있다. 그 이유는 우리는 머리 속으로 다음과 같은 과정을 거쳤기 때문이다.
- 관계 정의: 마동석 - 사탕 2개, 장첸 - 사탕 1개
- 문장 해석: 마동석이 장첸에게 사탕을 받았다. → 마동석 - 사탕 2 + 1 = 3개, 장첸 - 사탕 1 - 1 = 0개
- 방법: 위 과정을 위해 'operator indentification layer'를 제안하였다.
소개
(여러 가지 topic 에 대해 작성되어 있다보니, 다소 정렬이 아닌 나열에 가까운 느낌이다. 우선 문단을 순서대로 요약하였다.)
1. 최신 자연어 모델 사용: ELECTRA
2. 활용가능성
- 이 태스크를 해결하게 되면, 다양한 자연어 이해 능력, 수학 활용 태스크에 쓰일 수 있게 될 것이다.
- 예시: 세무 업무(tax affairs), 회계(accounting)
3. 역사
ㄱ. 1960년대부터 연구자들이 MWP 를 다루기 시작하였음.
ㄴ. 처음에는 수작업으로 특징을 추출하였으나(hand-crafted feature), 최근에는 자동적으로 특징을 추출하는 solution 이 많아짐.
ㄷ. 최근에는 machine learning 의 발달로, 연구자들은 RNN(recursive neural networks)이나 seq2seq(sequence-to-sequence incorporating natural language understanding models)와 같은 model architectures 를 도입해왔음.
ㄹ. 하지만 MWP 를 자동적으로 풀기 위해, 최근엔 'equation templates' 을 일반적인 접근으로 사용함.
- equation template: answer equation 의 일반화 버전을 의미함.
- 예컨대, 아래 예시의 1번 문항에서 ice cream 과 baseball cards 의 가격이 명시되어 있다. 이 가격을 그대로 사용한 것이 'answer equation'이다. 반면, 이 가격을 N에 관한 변수들로 치환하여 일반화한 게 'equation template' 이다.

- equation templates 을 사용하면, unlimited space 에서 restricted space 로 space of possible answer equation 이 줄어든다. 즉, 광범위한 범위가 아닌 제한된 범위 내에서 올바른 결과를 도출할 수 있도록 해준다는 것이다. 실제로, model testing 과정에서 성능 향상을 보여주었다.
4. template-based multitask generation (TM-generation) 제시
- 요약(abstact)에서 다룬 내용을 반복하기 때문에 생략함.
5. 실험과 분석
- MAWPS, Math23k datasets 을 활용하여 성능을 측정하였고, SOTA(state-of-the-art)에 도달함.
- 언어 모델이 상식(world knowledge)을 채워준다고 제안하였으며, 이를 더 높은 performance 를 보여주는 오류 분석을 통해 지지하였음.
- operation identification layer 제시: 숫자와 변수 사이의 관계를 추출하였음. 이는T-NTDNN 의 개선 버전임.
관련 연구
1. Solving mathematical word problem using template
- Kushman 이 template 을 사용하고 나서부터 많은 연구자들이 equation template approach 를 사용한다.
- 현재 쓰이는 methods 는 크게 'classification' 과 'generation' 으로 나뉜다.
ㄱ. classification
- model 이 training dataset 으로부터 equation template 을 학습함.
- 그래서 모델은 이전에 학습한 template 만 구별할 수 있음.
- 이로 인해, template 수를 제한하고자 함. 'slot' 을 활용하여, 다양한 equations 을 하나의 template 으로 묶었음.
- number 나 nouns 을 slotting 하였는데, number 만 slotting 한 게 가장 성능이 우수하였음.
- 하지만, slotting 은 information 을 masking 하는 issue 가 있음.
ㄴ. generation
- model 은 tokens 을 사용하여 직접적으로 equation 을 생성하는 법을 학습한다.
- model 이 학습 과정에서 심지어 보지 못한 데이터에 대해서도 생성하는 방법을 학습하기 때문에, classification 보단 더 나은 확장성을 띄고 있다.
- 현재 연구는 최적의 unit 을 찾기 위해 여러 시도를 하고 있다. 그 예시로 'recursive tree structures', 'simple sequences' 등이 있다.
→ 본 논문의 model 은 generation method 를 기반으로 개발되었다.
2. Methods for filling in a missing world knowledge
- 문제에 명시되지 않은 필수적인 information(world knowledge) 을 활용해야 한다.
- 그래서 BERT 와 같이 multi-domain corpus 로 사전학습된 model 을 fine-tuning 하여 사용한다.
- 실제로 BERT-based model 을 사용하여 성능을 올린 사례가 꽤 있다. 일부 논문에선 BERT 와 같은 language model 이 수리력, 수학적 이해능력을 함양하고 있다고 주장한다.
- 그러나, 숫자를 표현하는 토큰의 수가 적은 데이터로 사전 학습을 진행한 경우에는 오히려 성능이 감소할 수 있다. 실제로 소규모의 영화 대사 데이터로 사전학습한 모델이 사전학습되지 않은 모델보다 성능이 감소하였다. 그러므로, wikipedia 처럼 다양한 토큰이 담긴 dataset 으로 사전학습을 진행하는 것이 바람직하다.
- 또, 주어진 corpus 가 다양한 숫자 토큰들을 포함하더라도 그 토큰이 쓰인 맥락 역시 매우 다양하다. 그러므로, model 은 특정 task 를 다루기 위해 토큰을 잘 활용할 수 있는 방법을 고안해야 한다.
→ 본 논문의 model 은 위 과정을 위해 operation indentification layer 를 사용한다.
3. Methods for understand the relationship between numbers and variables
hand-crafted features
- 언어학자와 같은 domain experts 를 통해 내재된 relationships 을 추출 및 반영한다.
- 예시: ARIS 는 verb categorizer 를 사용하여 7가지 동사 유형으로 분류한다. 실제로, operator 와 numbers 사이의 연결을 파악하여 성능을 향상시킴.
- 그러나 설계 비용이 매우 비싸고, 특정 dataset 에 치우칠 수 있다. 이는 overfitting 을 야기하여 model 확장성을 제한한다.
automated features
- 위 한계를 극복하고자, 자동적으로 추출하기 위한 시도가 지속됨.
- 예시: deep neural solver 는 sequence-to-sequence model 을 사용하였음. 또, Bi-LSTM encoder 를 통해 피연산자 선택 과정과 연산자 선택 과정을 분리하기도 하였음. 최근에는 tree format 인 node 형태로 equation template 을 생성함.
- 더 최근엔, 'operator classification' task 가 제안되었음. 이 task 는 숫자와 변수 사이의 관계를 추출하고, 다양한 측면에서 이 관계를 추출할 수 있는 'multi-task learninig technique'을 제시함.
- multi-task learning technique: '연산자를 구분하는 방법', 그리고 'multi-task learning 과 함께 equation template 을 추출하는 방법'을 학습하면, 숫자의 일반화된 표현을 얻을 수 있다고 함. 이 방법으로 SOTA 를 찍음. 그러나 이 방법은 비용이 많이 들고, classification method 에만 의존적임.
→ 그러므로, 개선의 여지가 있다.
The TM-generation model
1. Input normalization
용어 정리
- INC (Index for numeric constants): 숫자/상수를 색인(index)를 가진 변수로 치환한 것
- NET (Normalized equation template): equation template 을 일반화한 것

과정
ㄱ. INC 생성
- question 에 존재하는 number 가 존재하면, 모두 그에 상응하는 INC 를 pairing 한다.
- 이때, 대문자 'N'을 사용하되, 등장하는 순서대로 index 를 할당한다.
ㄴ. postfix equation template 생성
- equation 을 postfix 형태로 변경한다.
- 숫자 대신 INC 로 치환한다.
ㄷ. NET 생성
- postfix equation template 에서 연산자를 OP token 으로 치환한다.
ㄹ. Partial NET 생성 (for T-MTDNN)
- NET 에서 OP token 이 모두 사라질 때까지 하나씩 삭제하며 만들어지는 모든 NET 을 의미한다.
2. Base model: T-MTDNN
: TM-generation model 은 T-MTDNN 의 개선 model 이라 먼저 알아둘 필요가 있다.
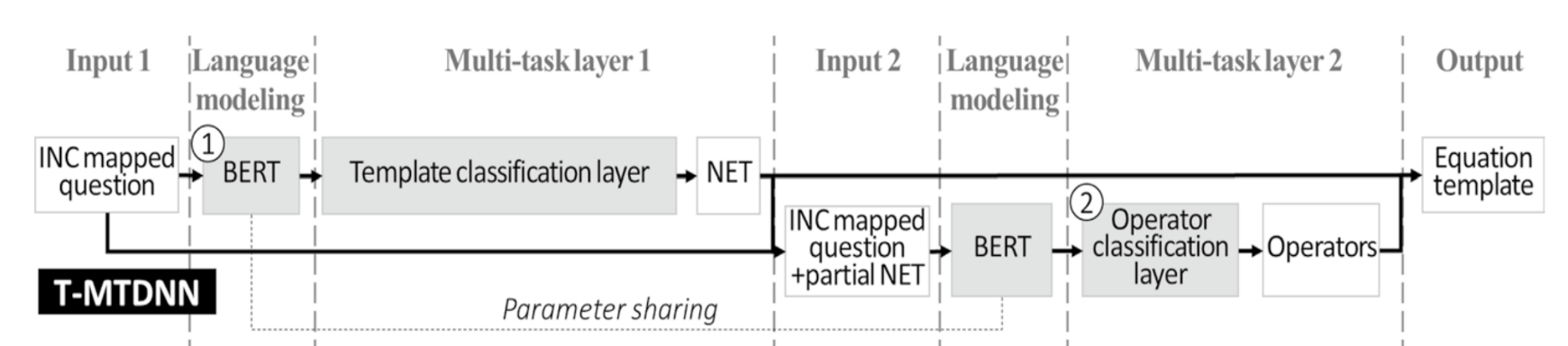
ㄱ. INC mapped question → BERT
- 목적: distributed representation 에 human progmatic language usage 와 world knowledge 를 반영한다.
- 입력: INC mapped question
- 출력: hidden-state vector
ㄴ. BERT → Template classification layer
- 목적: 가장 근접한/그럴듯한/유사한 NET 를 찾는다. (CLASSIFY)
- 입력: hidden-state vector
- 출력: NET
ㄷ. INC mapped question + partial NET → BERT
- 목적: ㄱ과 동일하다.
- 입력: INC mapped question + partial NET
- 출력: hidden-state vector
- 여기서 BERT 는 ㄱ 에 쓰인 model 과 동일하다. 즉 parameter sharing 이다.
ㄹ. BERT → Operator classification layer
- 목적: NET 에 존재하는 OP tokens 에 가장 근접한/그럴듯한/유사한 연산자를 찾는다. (CLASSIFY)
- 입력: [CLS] token at hidden-state vector
- 출력: operators
ㅁ. NET + operators → Equation template
- NET 에 위치한 OP tokens 를 operators 로 치환하면, equation template 이 완성된다.
3. TM-generation model
: 해당 논문에서 제시한 모델. T-MTDNN을 개선하였음.

ㄱ. INC mapped question → ELECTRA
- 목적: distributed representation 에 human progmatic language usage 와 world knowledge 를 반영한다.
- 입력: INC mapped question
- 출력: hidden-state vector
ㄴ. ELECTRA (encoder) → Transformer decoder
- 목적: 가장 근접한/그럴듯한/유사한 NET 를 생성한다. (GENERATE)
- 입력: hidden-state vector
- 출력: NET
- T-MTDNN 과 다르게, 훈련 과정에서 보지 못한 결과를 도출할 수 있다.
ㄷ. INC mapped question + NET → ELECTRA
- 목적: ㄱ과 동일하다.
- 입력: INC mapped question + NET
- 출력: hidden-state vector
- ㄱ 에 쓰인 model 과 동일하다. 즉 parameter sharing 이다.
ㄹ. ELECTRA → Operator identification layer
- 목적: NET 에 존재하는 OP tokens 에 가장 근접한/그럴듯한/유사한 연산자를 생성한다. (GENERATE)
- 입력: OP tokens at hidden-state vector
- 출력: operators
ㅁ. NET + operators → Equation template
- NET 에 위치한 OP tokens 를 operators 로 치환하면, equation template 이 완성된다.
차이점
ㄱ. model 변경: BERT → ELECTRA
- ELECTRA 가 language indestaing tasks(예시: question - answering) 에서 SOTA 를 달성하여 이 task 에서도 좋은 성능을 기대하였음.
ㄴ. Operation identification calculation process
- input format: T-MTDNN 에서는 [CLS] token 을 사용한다. 물론, 문장 전체를 함축적으로 담고 있는 벡터로서, classification 등에 활용되는 중요한 정보 중 하나다. 하지만 바로 이 점 때문에 OP token 수만큼 pipeline 을 돌려야 한다. 반면, TM-generation 에서는 그럴 필요가 없다. OP tokens을 한번에 처리할 수 있어 효율적이다.
- directional information: T-MTDNN 에선 [CLS] token 을 사용한다. 이는 간접적으로 정보를 함축하고 있는 hidden state vector 다. 아무리 전체 문장을 반영하고 있떠라도, 문장의 어떤 부분을 근거로 추측하는지 불명확하다. 반면 TM-generation 에선 OP token 을 사용하는데, 이는 직접적으로 정보를 활용하기 때문에 더 안정성이 높다고 볼 수 있다.

실험
benchmark dataset
ㄱ. MAWPS
[
{
"iIndex": 1,
"sQuestion": "Joan found 70.0 seashells on the beach . She gave Sam some of her seashells . She has 27.0 seashells . How many seashells did she give to Sam ?",
"lEquations": [
"X=(70.0-27.0)"
],
"lSolutions": [
43.0
]
},
...
]
ㄴ. Math23k
{
"id":"1",
"original_text":"镇海雅乐学校二年级的小朋友到一条小路的一边植树.小朋友们每隔2米种一棵树(马路两头都种了树),最后发现一共种了11棵,这条小路长多少米.",
"segmented_text":"镇海 雅乐 学校 二年级 的 小朋友 到 一条 小路 的 一边 植树 . 小朋友 们 每隔 2 米 种 一棵树 ( 马路 两头 都 种 了 树 ) , 最后 发现 一共 种 了 11 棵 , 这 条 小路 长 多少 米 .",
"equation":"x=(11-1)*2",
"ans":"20"
}

baseline models
ㄱ. TSN-MD
- Teacher - Student approach: 여러 개의 decoder 를 사용하여 다양한 결론을 도출한 다음, 가장 높은 beam score 를 가진 결론을 채택하는 방식이다.
- 이 방식은 학생들간의 학생 과정을 정규화할 수 있다.
ㄴ. Griffith and Kalita
- Transformer model
- 본 논문에 쓰일 model 과 동등 비교가 불가능하다. 공표되지 않은 test dataset 을 사용하였고, ramdom sampling 하였기 때문이다. 그래서 불가피하게 five-fold cross-validation 을 통해 성능 비교를 하기로 하였다.
ㄷ. T-MTDNN
구현
대상: T-MTDNN with operation identification, TM-generation models

- Machine learning library: pytorch 1.6
- Transformer library: ELECTRA-base, Chinese-ELECTRA-base (Math 23k 가 중국어 데이터라서 사용함)
- operation identification layer: single linear layer
- template generation layer: a single template generation layer
- Transformer decoder: transformer decoder with six layers. 각각의 decoder layer 는 head 8개, multi-head attention 이 2개다. 그리고 intermediate layer 의 output 크기는 2048이다.
hyperparameter
- optimizer: Adam

- scheduler: linear warm-up scheduler with warm-up step ratio = 0.1
- learning rates: ranging from 3 * 10^(-5) to 2 * 10^(-4)

- batch size: 16 problems in a batch
- cross entropy loss with label smoothing approach
- beam search: beam size = 3
- environment: Google Colab, local PC with 64 GB RAM and RTX 2070 Super and RTX 2080 Ti, a local server with 192 GB and two RTX Quadro 8000
결과 및 토론
2개의 dataset 에서 모두 SOTA 를 달성하였다.

ㄱ. Analysis of filling in world knowledge
ablation study 진행: language model 의 유무를 비교하는 실험 설계하였다. 'OP'라 적힌 건, language model 을 활용하지 않은 것. 즉, World Knowledge 가 반영되지 않은 경우를 의미한다. 대조군을 통해 어떤 성능 차이를 보이고, 그 차이를 분석하여 정당성을 부여하고자 한다.

- 정확도 향상이 2개의 dataset 모두에서 10% 이상 나타나고 있음.
- World Knowledge(이하 WK) 가 필요한 문제들 사이에서도 정확도가 상승한 것을 확인할 수 있다.
- 다만, Math23k 에선 20 문제를 더 맞출 수 있게 된 반면 MAWPS 에선 4문제 정도 개선밖엔 없었다. 그 이유로 Math23k 에서 WK 를 필요로 하는 문항수가 5235개인데 MAWPS 에서는 겨우 189개뿐이다. 실제로 dataset 비율에서도 MAWPS 의 20% 정도가 WK 를 필요로 하는 문제인 반면, Math23k 는 무려 70%에 달한다. 이로 미루어 보아, MAWPS 에서는 WK 를 배우고 활용할 충분한 기회가 주어지지 못해서 발생한 것으로 추정된다.
ㄴ. Analysis of understanding the implied relationship
ablation study 진행: operatior identificatinon task 의 유무를 비교하는 실험 설계하였다. 'PG'란 pure generation model 로서 순수하게 바로 생성하는 모델이다. 이는 operation identification task 가 얼마나 숫자와 변수 사이의 관계를 잘 이해하고 반영하고 있는지를 비교하기 위해 쓰인다.
평가지표

1) Problem solving accuracy
2) Correct NET(CN): NET 을 올바르게 생성한 문제의 개수
3) correct operator(CO): OP 를 올바르게 생성한 문제의 개수
→ 전반적으로 성능이 개선된 모습을 보여준다. 그러므로, 논문에서는 operation identification layer 가 숫자와 변수 사이의 관계를 파악하고, 이를 반영하고 있다고 결론을 지었다.
결론
1. 논문에서는 2가지 challenge 를 성공적으로 다루었으며,
- world knowledge 를 반영하여 문제 풀이 능력을 향상시킨다.
- 문제에 주어진 숫자와 변수 사이의 관계를 파악하도록 한다.
2. 그 결과 MAWPS 에선 85.2%, Math23k 에선 85.3% 의 성능을 거두어 SOTA 를 달성하였다.
3. 1번째 challenge 를 해결하고자, 충분한 데이터로 사전 학습된 자연어 모델을 활용하였으며,
4. 2번째 challenge 를 해결하고자, 개선된 버전의 operator identification 을 선보였다.
5. 그리고 논문에선 실험과 ablation study 를 통해 분석 및 결과를 제시했다.
의견
1. [비판적 관점] 사전학습 모델을 거치는 것이 world knowledge 를 채웠다고 볼 수 있을까?
- 본 논문에서는 상식(world knowledge)를 필요로 하는 문항의 정답률 및 성능 향상을 근거로 이 과정의 정당성을 부여할 뿐이다. 결과론적인 해석일 수 있다.
- 다른 이유로 성능이 올랐을 가능성도 있다. 그 이유를 밝히는 것은 매우 까다롭고 어려운 일이긴 하다.
2. [제안적 관점]
추후 정리할 내용
- BERT
- ELECTRA
- ablation study
- Adam optimizer
- label smoothing



