해당 포스팅은 학습 차원에서 아래 글을 의역하여 작성합니다. 도입부와 배경은 가볍게 다루되, 이해해야 할 부분은 최대한 자세히 담아보고자 합니다.
https://huggingface.co/blog/hf-bitsandbytes-integration
A Gentle Introduction to 8-bit Matrix Multiplication for transformers at scale using transformers, accelerate and bitsandbytes
A Gentle Introduction to 8-bit Matrix Multiplication for transformers at scale using Hugging Face Transformers, Accelerate and bitsandbytes Introduction Language models are becoming larger all the time. At the time of this writing, PaLM has 540B parameters
huggingface.co
소개

- 언어 모델이 점점 증가해 이제는 540B까지 도달했다.
- 이로 인해 대기업을 제외하고는 GPU 사용이 버겁다.
- 예컨대, BLOOM 176B을 학습하는데 80GB A100 GPU가 8개 필요하다.
- A100 1개당 가격이 15,000$ 로 오늘 기준 1900만원이다.
- 이런 문제를 극복하기 위해, 모델 경량화, 양자화, distillation 등 다양한 기법이 등장했다.
- BigScience community 에서는 Int8 Inference가 성능을 하락하지 않는다는 걸 발견했다.
- Huggingface는 이 점에 착안하여, transformer 라이브러리에서 LLM.int8() 을 사용할 수 있도록 했다.
머신 러닝에서 쓰이는 데이터 유형

1) FP32, FP16
- 컴퓨터 공부를 하는 분들이라면 다들 들어봤을 것이다. 처음 들어봤다면, 검색해서 기초를 알아오길 추천한다.
- Range: exponential 로, 지수 범위를 나타낸다.
- Precision: mantissa 로, 소수점 범위를 나타낸다.
- Sign: 음수인지 양수인지를 표현한다.
- 보통 컴퓨터는 이렇게 IEEE 32-bit 표준을 따르며 실수(float)를 표현해왔다.
- FP16은 그림을 보면 알 수 있듯이, 더 작은 자료형인 16-bit 로 실수를 표현하는 것뿐이다.
- 여기까지는 기초적인 단계다.
2) BF16
컴퓨터는 결국 이진법으로 모든 것을 표현하기 때문에 우리 눈에 완벽해보여도 실제로 표현할 수 있는 범위의 한계가 있다. 예컨대, FP16은 FP32보다 적은 비트를 사용하기 때문에 표현할 수 있는 수의 범위가 제한적이다. 예컨대, 10,000 * 10,000 = 100M 이지만, FP16에서는 표현할 수 없다. 이 경우엔 'NaN' 으로 표기되며, 딥러닝 도중에 이런 계산이 발생했다면 정상적인 학습(forward, backward, loss computation)에 문제가 생긴다.
이를 극복하기 위해, 만들어진 자료형이 바로 'BFLOAT16' 이다. 똑같이 16-bit을 사용하지만, FP16에 비해 Range의 범위를 늘리고, Precision을 줄였다. 이게 무엇을 의미할까? 바로 FP32의 Range 를 모두 표현할 수 있다는 점이다. 줄여야 했던 16 bit 를 모두 Precision 에서 감당하고, Range 는 유지한 셈이다.
3) TF32
- NVIDIA에서도 새로운 자료형을 제안했다.
- Range 는 BF16 을 따르고, Precision 은 FP16 을 따르는 자료형이다. 각각의 크기를 계승했다.
- 그래서 19비트인데, 특수한 연산에만 쓰인다고 한다.
- (개인적으로 19비트라서 어떻게 쓰일지 모르겠고, 여기서는 가볍게 이런 게 있구만 정도로만 짚으면 되는 것 같다.)
4) INT8
- FP32 는 full precision (4 bytes) 이라고 부르고, FP16, BF16 은 half-precision(2 bytes) 이라고 불린다.
- 그 다음으로 INT8 이 위치하는데, [0, 255] 혹은 [-128, 127] 의 범위를 갖는다.
- 크기는 겨우 1 byte 인 셈이다.
- (기초적인 자료형들과의 비교를 위해, 간단히 블로그에 언급한 것 같다. 뒤에 상세히 나온다.)
모델을 학습/추론할 때 쓰이는 자료형
- 이상적으로는 FP32를 처음부터 끝까지 사용하는 것이 좋다.
- 하지만 BF16/FP16 을 사용하면 2배 이상 빠르고, 정확도도 유지할 수 있다.
- forward 및 backward 할 때는 FP16/BF16 을 통해 속도를 증진할 수 있기 때문이다.
- (혹시 이 부분에 대해 처음 들었다면, FP16에 관한 논문이나 엔비디아 블로그의 글을 꼭 읽어보시길 추천합니다.)
그렇다고 해도 여전히 많은 메모리가 쓰이고 있다. 예컨대, BLOOM 의 파라미터 크기를 구해보자. 176 * (10 ** 9) X 2 bytes (half - precision) = 352GB ! 여전히, 우리가 일반적으로 사용하는 GPU에 올리기엔 부담스럽다. 이 문제를 해결하기 위해, 양자화(quantization)가 등장했다.
모델 양자화
- 32 bit 에서 16 bit 로 줄이면서 성능을 유지했지만, 그 이상 bit 를 줄이면 성능이 감소한다.
- 이 문제를 해결하기 위해 '8-bit quantization' 을 제시한다.
- 단순히 bit 를 버리는 것은 아니다.
양자화는 손실을 감수해야 한다
양자화는 한 자료형에서 다른 자료형으로 변환하면서, 필수적으로 '올림(rounding)'을 거친다. 예컨대, [0, 9] 를 표현하는 자료형 A 와 [0, 4] 를 표현하는 자료형 B가 있다고 가정하자. 자료형 A 에서는 '4' 는 자료형 B에서 '2'가 된다. 범위가 절반이니, 반으로 나눴다고 생각하면 편하다. 하지만 '3'은 어떨까? '3'은 '1'과 '2' 사이에 놓이는 것이 합당하지만, 자료형 B는 그걸 표현할 수 없기 때문에 어쩔 수 없이 '2' 로 표현해야 한다. 또 다른 문제가 있다. '3'과 '4'는 자료형 B로 표현하면 모두 '2'가 된다. 이렇게 양자화는 정보의 오염을 수반하는 과정(noisy process)임을 기억해야 한다.
zero-point quantization
양자화에는 2가지 방식이 있는데, 모두 실수를 정수범위로 바꾼다. 예컨대, zero-point quantization 은 내 데이터의 범위가 -1 ~ 1 인데, -127 ~ 127 로 양자화를 진행하고 싶다면, 127 을 곱해서 올림을 한다. 0.3 이라면 0.3 X 127 = 38.1 이니, 38로 양자화되는 셈이다. 다시 역으로 되돌릴 땐, 38 / 127 = 0.2992 로 0.008 의 오차를 갖게 된다. 이런 오차는 작아보여도 누적되면 점점 커져서 모델의 성능이 악화를 가져온다.
absolute maximum quantization
한편, absolute maximum quantization 다음과 같은 순서로 이뤄지는데 그림을 따라 글을 읽으면 좋다.
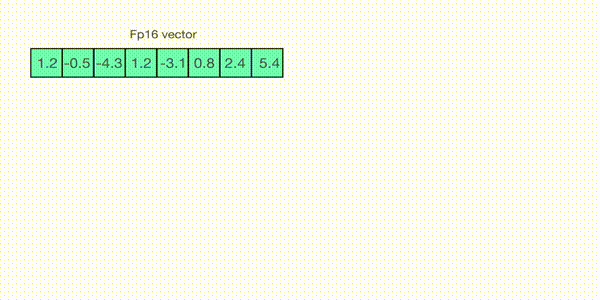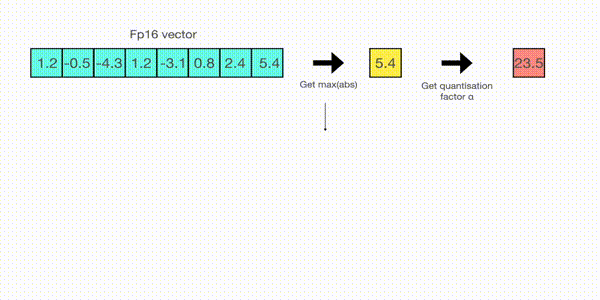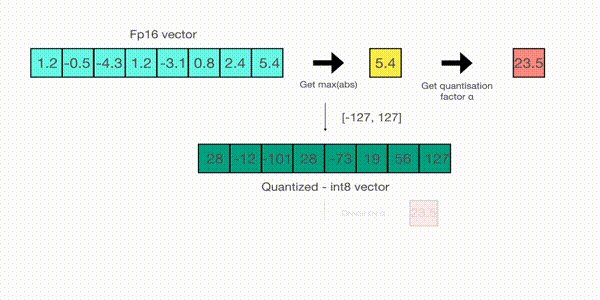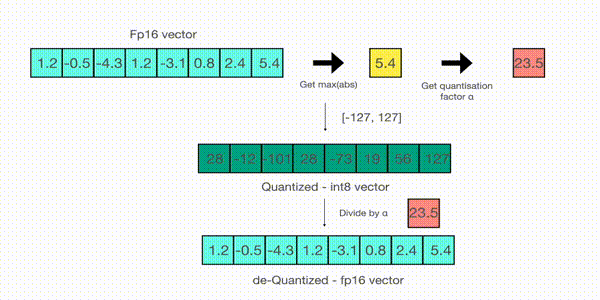
- 1. 벡터에 absmax 를 취해서 절대값이 가장 높은 값을 구한다. 여기서는 5.4 다.
- 2. 표현하고 싶은 범위의 최댓값인 127 을 5.4 로 나눈다. 23.5 가 나온다.
- 3. 모든 벡터에 23.5 를 곱한다. 그러면, 1과 2에 의해 모든 값의 범위가 -127 ~ 127 에 머물게 된다.
- 4. 원래대로 돌리고 싶으면 다시 23.5 를 나누면 된다.
- 이 방식도 당연히 손실이 생길 수 있다.
이 방법을 행렬 곱 연산에서도 사용할 수 있다. 행렬 A, B 를 곱해서 A * B = C 를 만든다고 가정하자. 이때, A 는 row 별로 양자화를 진행하고, B 는 column 별로 양자화를 진행한다. 그리고 A 와 B 를 곱해서 C 를 만들면 되지 않겠는가?
(이 정도의 설명 후, 자세한 건 논문을 읽어달라고 하셨다.)
https://arxiv.org/abs/2208.07339
LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale
Large language models have been widely adopted but require significant GPU memory for inference. We develop a procedure for Int8 matrix multiplication for feed-forward and attention projection layers in transformers, which cut the memory needed for inferen
arxiv.org
하여튼, 이 방법을 쓰면 성능이 떨어져야 하지만, LLM.int8() 기법은 성능 하락 없이 BLOOM 같은 거대 모델에게도 적용할 수 있는 기법이라고 한다.
LLM.int8(): 거대언어모델을 위한 성능하락 없는 행렬 곱 연산

- 우선 냅다 LLM.int8() 연산이 어떻게 발생하는지 보겠다.
- 범위를 벗어나는 값을 outlier 라 부르며, non-outlier 와 outlier 를 구분하여 계산하는 것이 핵심이다.
- 1. input hidden states 에서 outlier 와 non-outlier 를 구분한다.
- 노란색이 outlier 이고, 청록색이 non-outlier 다.
- 2. outlier 는 FP16 으로 연산하고, non-outlier 는 int8 로 연산한다.
- (이 과정을 통해서 outlier 만 정확하게 계산해서 오차를 없애는 것으로 보인다.)
- 3. non-outlier 는 dequantization 을 통해 원래 값을 구하고, outlier 는 FP16 의 결과를 그대로 사용한다.
outlier features 의 중요성
- 기본적으로 6B 이 넘는 모델이면, 일반적인 양자화를 진행할 경우 손실이 발생한다.
- 이건 작은 모델에서도 그렇고, 트랜스포머 모델 특성상 오류가 전파될 위험이 매우 높다.
- 그러므로, mixed-precision decomposition 은 이런 outlier들에게 특히 효과적이다.
행렬 연산을 들여다보다
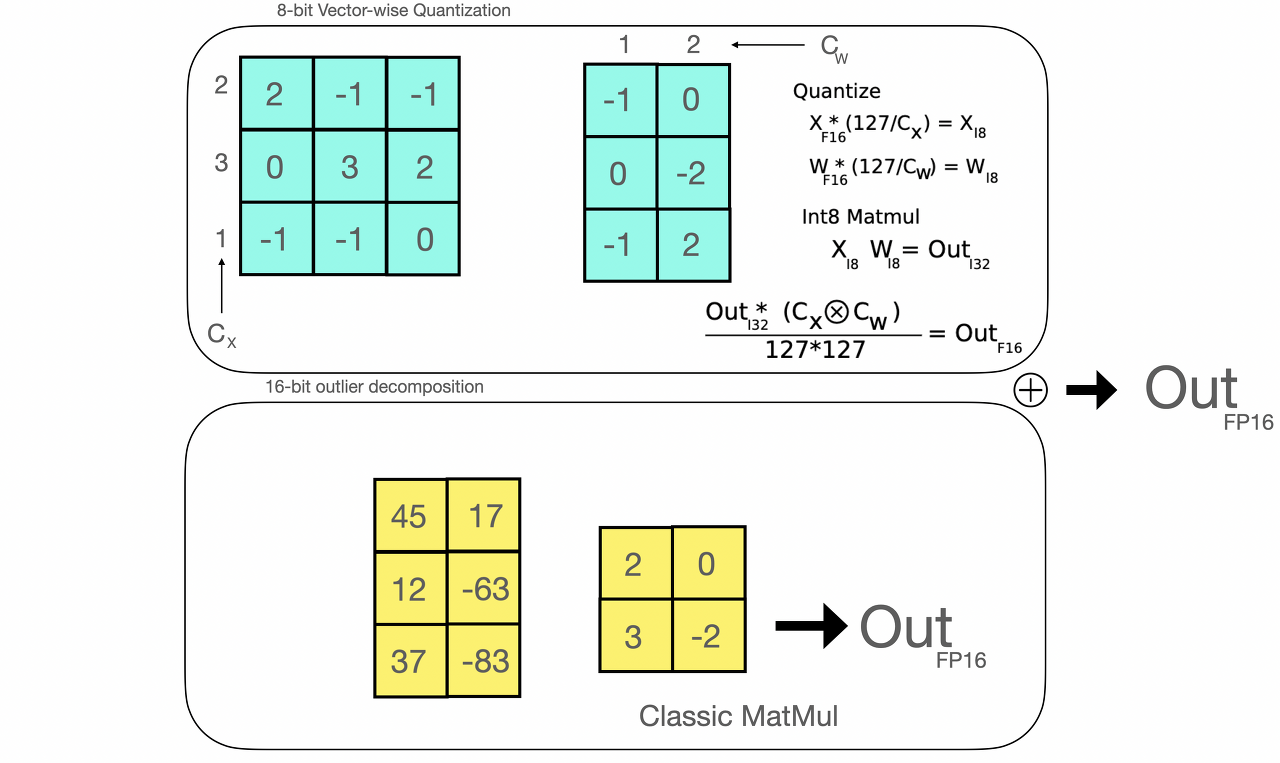
- 앞서 말했듯, 특정 custom threshold 를 통해서 outlier 를 추출하고 연산한다.
- 여기서 6 을 theshold 로 잡았을 때, inference 성능이 유지된다는 걸 확인할 수 있었다.
- 그러므로, A 는 row, B는 column 하게 양자화를 진행한 뒤, 행렬 곱 연산을 실행하면 된다.
실험 결과
아래 표를 보면 성능 하락이 거의 없다는 걸 확인할 수 있다.
OPT-175B:
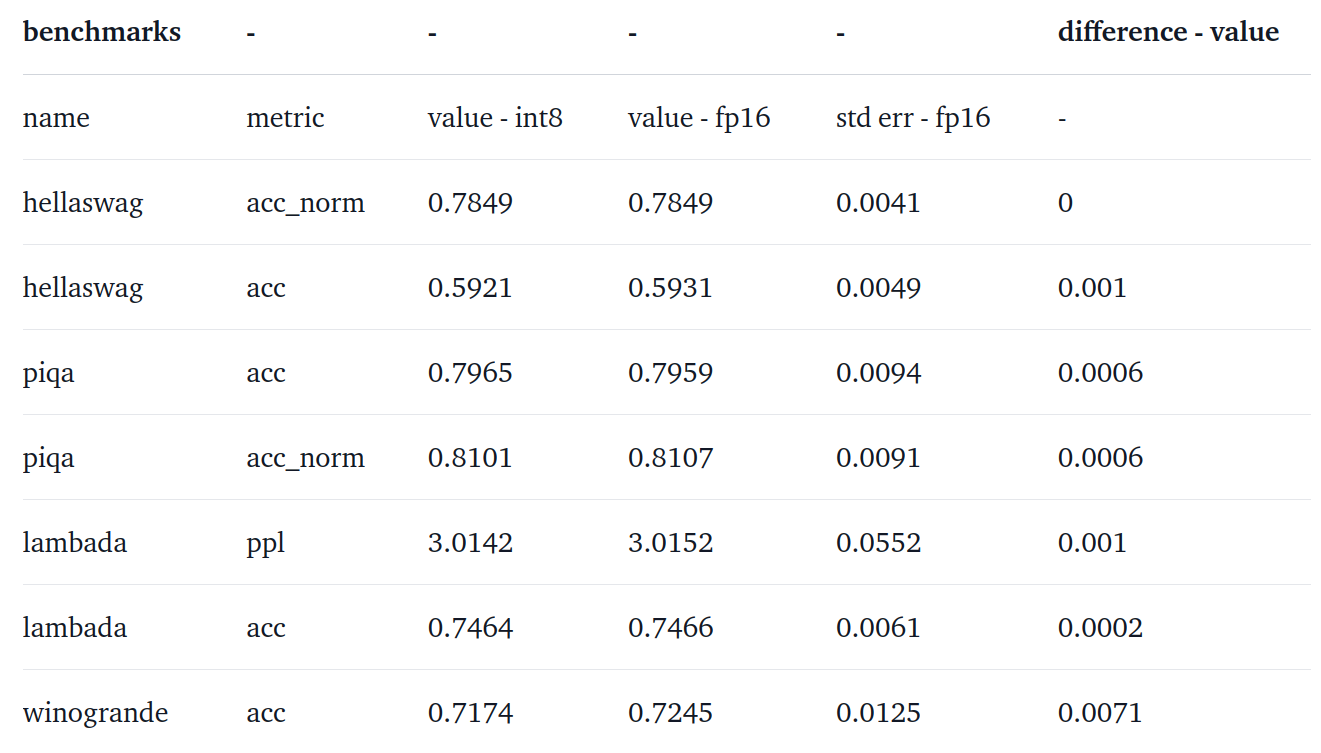
BLOOM 176B:
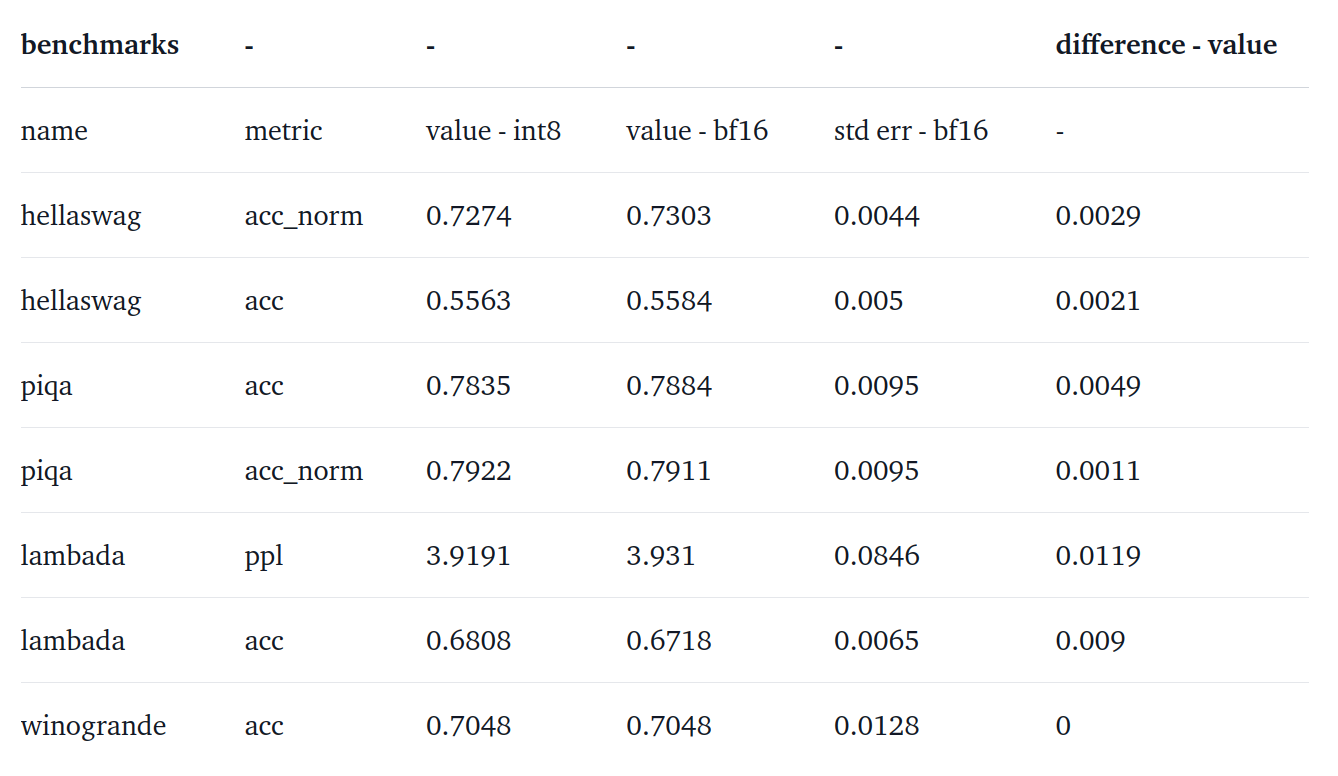
이 모델들, 속도는 어떨까?
애초의 목적은 성능 하락 없이 거대모델의 접근성을 높이자는 것이었다. 하지만, 매우 느리다면 이 방법이 효과적이라고 볼 수는 없다. 그래서 실험을 통해서 얼마나 속도가 하락하는지 확인했다.
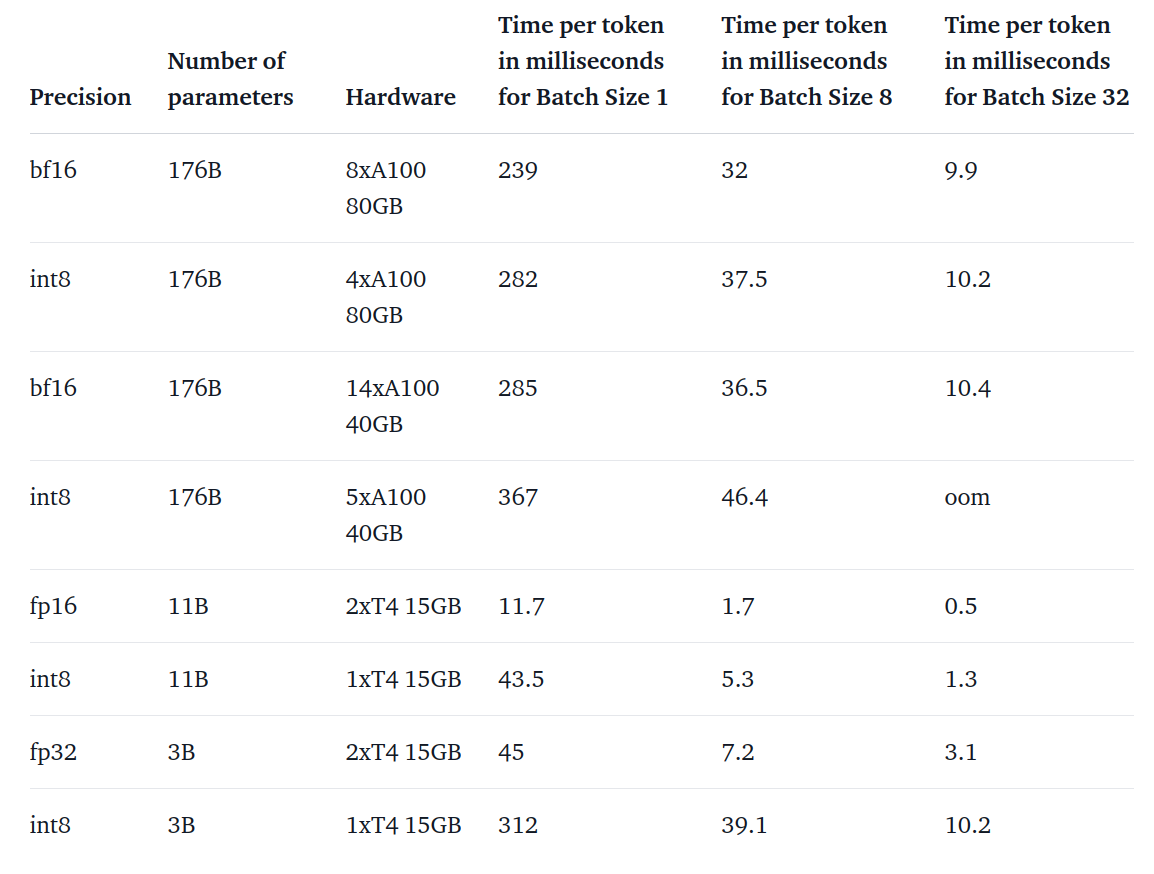
- BLOOM 176B: fp16보다 15 ~ 23% 더 느려짐.
- 작은 모델일수록 느려지나, 이 문제에 대해 인지하고 있고 추후에 개선한다고 함.
뒷 내용은 코드 상으로 활용하는 방법이라 huggingface 블로그를 이어서 읽으면 될 것 같다.
https://huggingface.co/blog/hf-bitsandbytes-integration
A Gentle Introduction to 8-bit Matrix Multiplication for transformers at scale using transformers, accelerate and bitsandbytes
A Gentle Introduction to 8-bit Matrix Multiplication for transformers at scale using Hugging Face Transformers, Accelerate and bitsandbytes Introduction Language models are becoming larger all the time. At the time of this writing, PaLM has 540B parameters
huggingface.co
'NLP > huggingface' 카테고리의 다른 글
| [huggingface🤗] OSError: You are trying to access a gated repo (0) | 2024.03.22 |
|---|---|
| [huggingface🤗] Prompting? PEFT? 총정리 (3) | 2023.08.09 |
| [huggingface🤗] Making LLMs even more accessible with bitsandbytes, 4-bit quantization and QLoRA (0) | 2023.06.27 |
| [huggingface🤗] How to generate text #2 (1) | 2022.12.28 |
| [huggingface🤗] How to generate text #1 (0) | 2022.12.09 |



