논문명: Dynamic Prompt Learning via Policy Gradient for Semi-structured Mathematical Reasoning (ICLR 2023)
논문링크: https://arxiv.org/abs/2209.14610
Dynamic Prompt Learning via Policy Gradient for Semi-structured Mathematical Reasoning
Mathematical reasoning, a core ability of human intelligence, presents unique challenges for machines in abstract thinking and logical reasoning. Recent large pre-trained language models such as GPT-3 have achieved remarkable progress on mathematical reaso
arxiv.org
아이디어만 정리합니다
핵심
- 상황: In Context Learning 할 때, 예제를 K개 뽑아서 함께 넣어주면 잘 한다.
- 문제: 어떻게 K개를 뽑는 게 좋을까? 이건 In Context Learning 에서 Demonstration Selection 이라고 부른다.
- 해결책: K개를 뽑는 classifier 를 강화학습을 통해 학습한다.
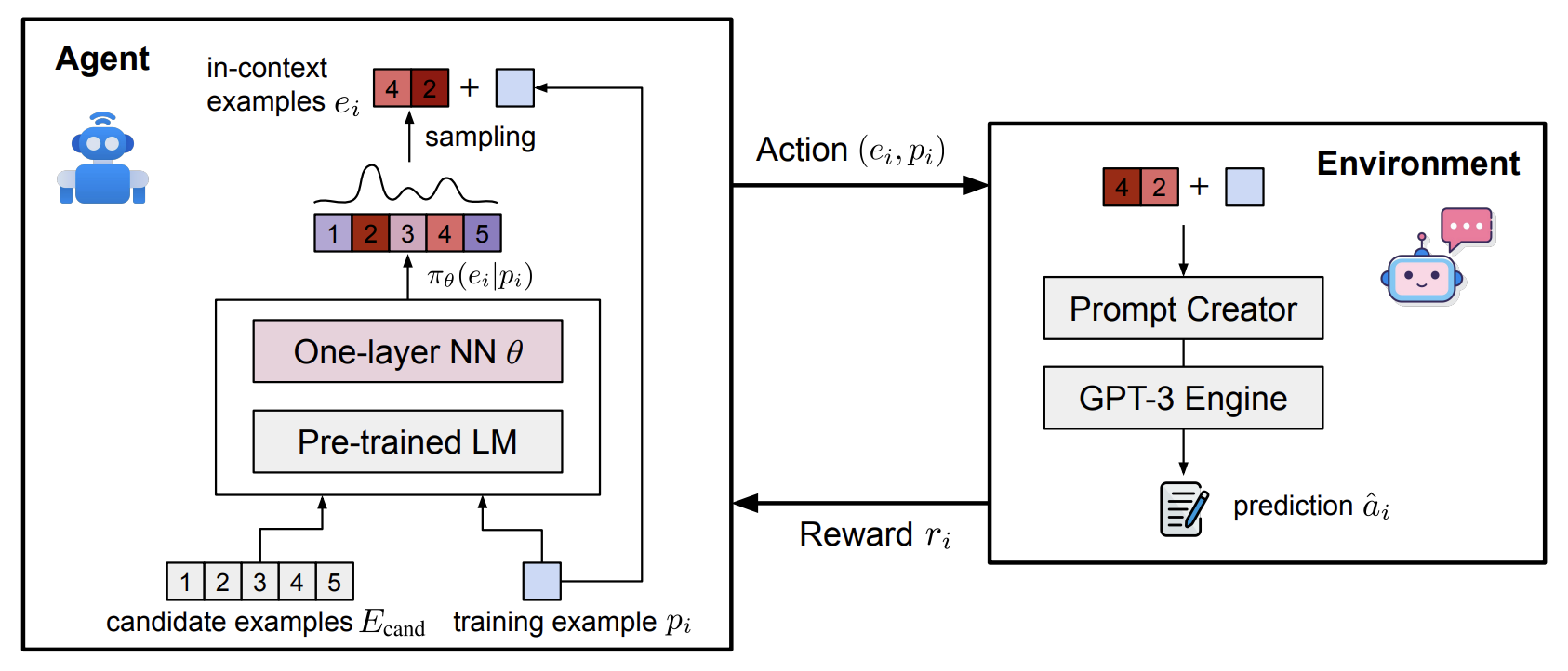
- Pi: 내가 풀고 싶은 문제
- Ecand: 함께 넣을 예제 후보
방법
- 각각(문제와 예제후보들)을 BERT로 먼저 임베딩한다.
- Layer 1개로 임베딩을 한번 더 감싼다.
- Softmax 로 확률을 구한다.
- Sampling 을 통해 뽑는다 (가장 높은 확률 K개를 뽑는 것도 궁금한데, 왜 sampling 만 했지?)
- 뽑은 예제 K개와 문제를 함께 넣어 모델이 정답을 맞추는지 확인한다.
- Exact Matching 을 통해 맞추면 1, 틀리면 -1 의 보상을 제공한다.
의견
- ChatGPT 처럼 정답이 없는 생성 태스크는 인간의 선호도나 BERTSCORE로 reward 를 준다.
- 반면, 수학 문제처럼 정답이 있는 경우엔 맞췄을 때와 틀렸을 때에 따라 reward 를 줄 수 있다.
- 먼 훗날엔, 아깝게 틀린 경우와 맞아도 풀이가 틀린 경우도 구분할 수 있지 않을까.
'NLP > 논문이해' 카테고리의 다른 글
| [논문이해] CODEFUSION: A Pre-trained Diffusion Model for Code Generation (0) | 2023.11.05 |
|---|---|
| [논문이해] Neural Text Generation with Unlikelihood Training (0) | 2023.11.02 |
| [논문이해] BLEURT: Learning Robust Metrics for Text Generation (0) | 2023.09.22 |
| [논문이해] Active Retrieval Augmented Generation (0) | 2023.09.15 |
| [논문이해] Should You Mask 15% in Masked Language Modeling? (0) | 2023.09.14 |



