[논문이해] What learning algorithm is in-context learning? Investigations with linear models

논문명: What learning algorithm is in-context learning? Investigations with linear models

논문링크: https://arxiv.org/abs/2211.15661

What learning algorithm is in-context learning? Investigations with linear models

 

선정 이유

• 리뷰어들의 평이 좋고, 유명인들도 추천함
• 구글과 같이 고수들이 낸 논문임
• In Context Learning 의 원리를 수식적으로 파헤치는 논문임. 보통 In Context Learning 을 분석한다 해놓고, 요소의 유무를 통한 ablation study 만 하지, 수식적으로 파헤치는 논문은 거의 없음. (왜냐면 매우 어려우니까...)
• 내가 읽어본 논문 중 가장 압도적으로 어렵다...

---

논문의 큰 그림

: 아무리 생각해도 논문이 어렵기 때문에 간단히 무엇을 하는지 보여주고 그 후에 상세히 들어가도록 하겠다.

 

• 이렇게 입력과 그에 따른 정답을 함께 예시로 제공해주는 걸 In Context Learning 이라고 한다.
• 여기서는 예제를 x1, f(x1) 을 제공할 때, x2 를 묻는 상황을 가정한다.

 

• 그러면 transformer decoder 에 의해 위 상황이 펼쳐진다.
• 예제 1개를 제공할 때, x2 를 예측하는 상황이다.
• 이때, 저자가 증명하고자 하는 내용은 오른쪽 파란 글씨다. X1 을 linear regression 한 결과를 back propagation 한 matrix 가 x2를 예측할 때 쓰인다. 즉, x1 을 back propagation 한 효과를 낼 수 있다는 게 이 논문의 핵심이다.
• 아래 과정을 가볍게 보며 왜 그렇게 할 수 있는지 이해하면 된다.

 

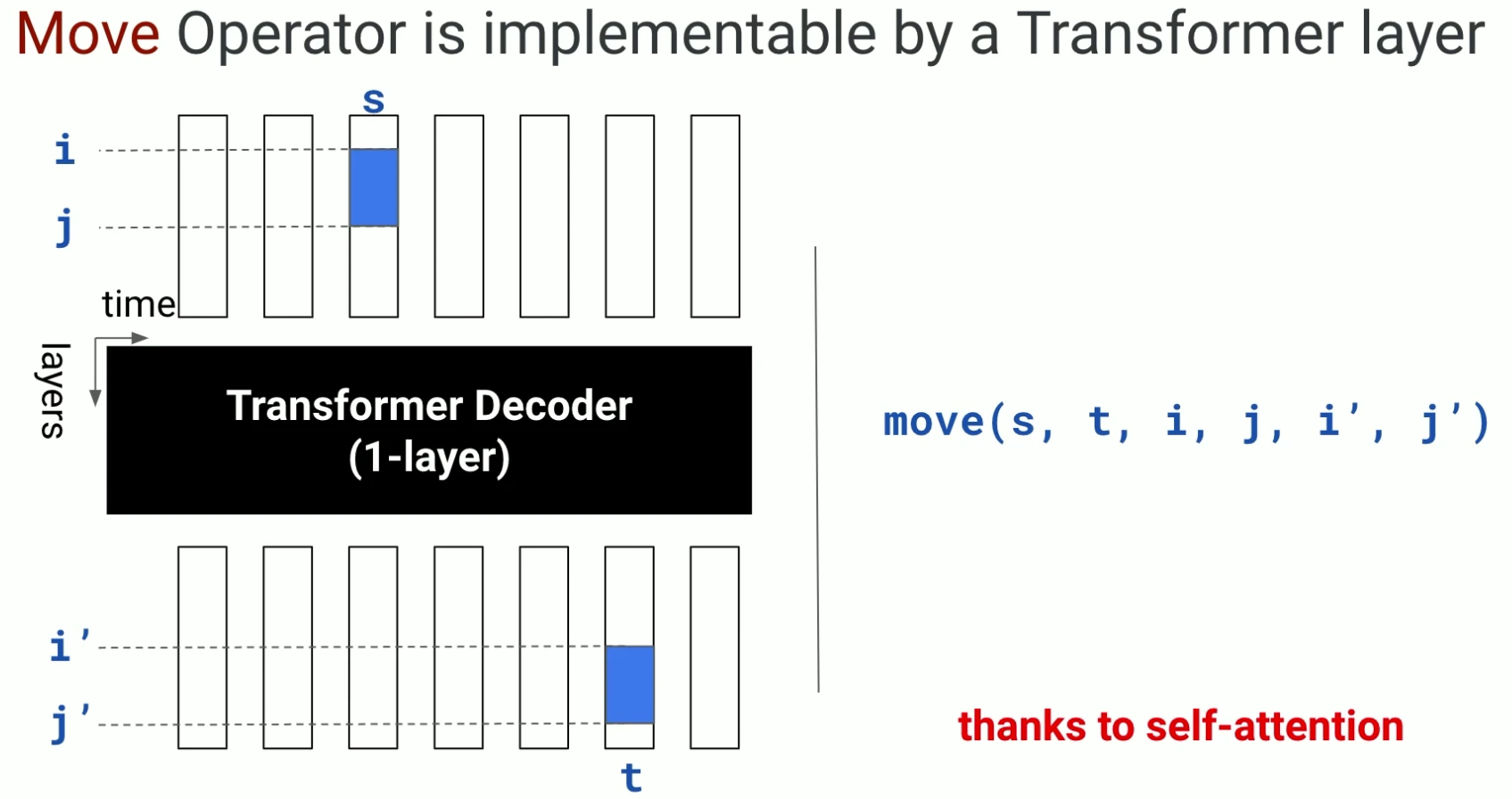
• 먼저 값을 옮기는 연산을 실행한다.
• x1 의 1,2번째 성분이 결과의 1,2번째 성분으로 복사되었다.
• 이건 실제로 transformer decoder 로 구현가능하다고 한다.

 

• 이런 연산도 가능하다고 한다. 그냥 그렇구나 하고 넘기자.

 

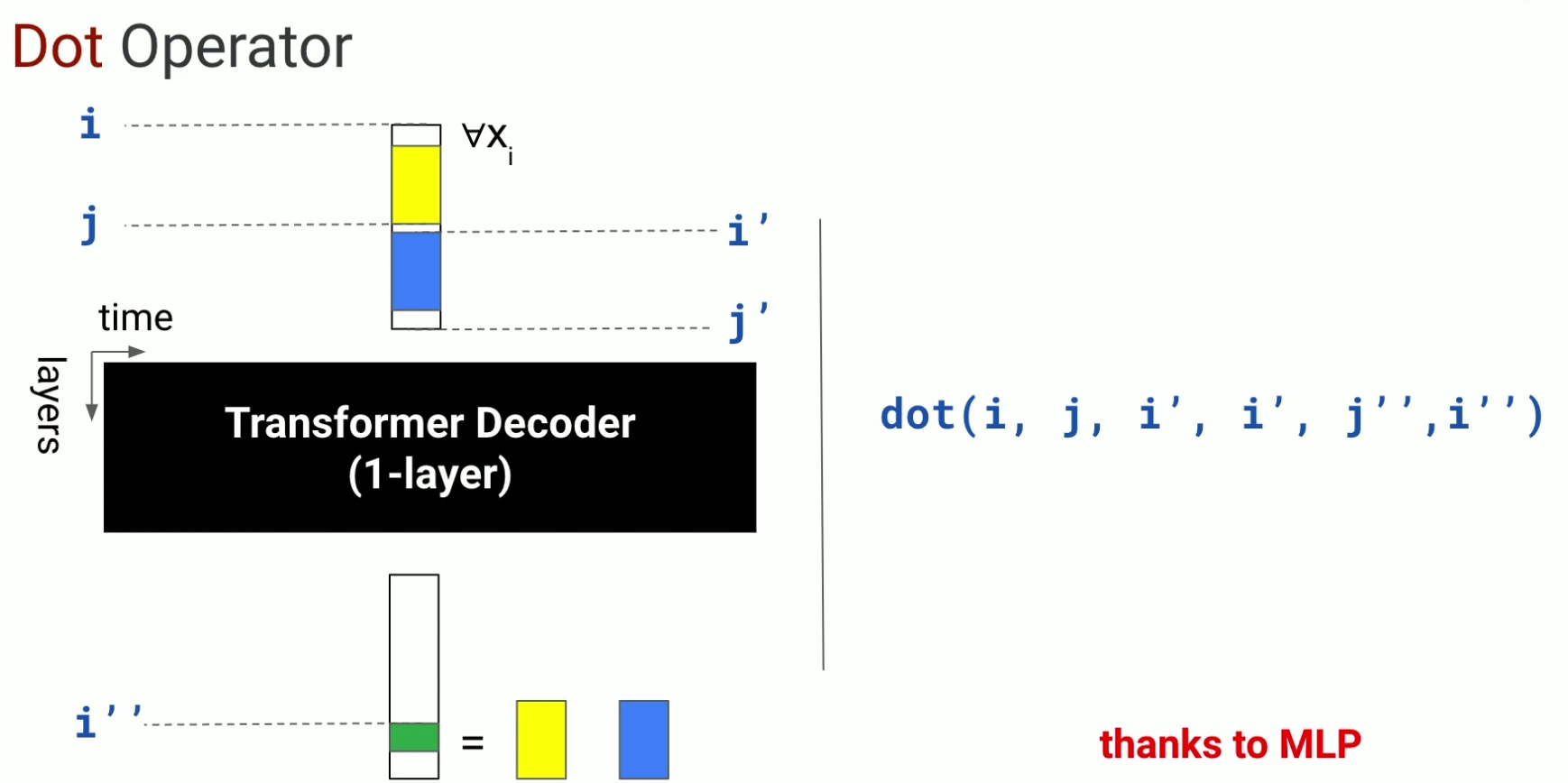
• 이 연산도 마찬가지다.
• 결론적으로 이리 저리 계산하다보면, 아래와 같은 결론이 나온다.

• 즉, back-propagation 을 통한 parameter update 가 일어나지 않았지만
• transformer decoder 만으로 다양한 연산이 가능해서
• 결론적으로 back-propagation 과 동일한 값을 낼 수 있다
• 가 핵심이다.

 

이제, 이 논문의 흐름은 과연 transformer decoder 가 저런 연산이 가능한지 확인하면 된다.

 

논문의 흐름

: 내가 이 논문의 흐름을 정리하기 위해 만든 그림이다. 논문은 이해를 돕기 위해 이 순서를 자유롭게 바꾸지만, 결국 이 흐름을 잡는 게 가장 핵심인 것 같아 정리했다.

 

• 먼저, 네모는 각각 요소를 의미하며 총 4개다.
• 우리는 위 그림에서 1번과 3번이 동치이면, 7번에 의해 4번을 구현할 수 있다는 큰 그림을 보았다.
• 사실은 위 과정처럼 1 ~ 4번을 이해하고, 5 ~ 7번 증명을 해야 한다.
• 색깔은 이해의 난이도를 의미한다.
• Transformer algorithm, linear regression: 워낙 유명하고 기초인 만큼, 쉽다는 의미로 초록색을 부여했다.
• mov, mul, div ,aff: 낯설지만 그래도 읽으면 금방 이해할 수 있어서 노란색을 부여했다.
• RAW operator: 낯설고 어렵다. 하지만 이걸 통해 증명이 간단해진다고 한다. 빨간색으로 표기했다.
• 5, 6, 7: 사이사이에 화살표는 동치로 표현가능하다를 의미하며, 모두 어렵기 때문에 빨간색을 넣었다.
• 특히 5번 증명은 며칠에 걸쳐 읽어도 이해가 되지 않아 포기했다. 궁금한 사람들은 논문의 18 ~ 25 페이지를 읽어보길 바란다.
• 내 기억이 맞다면, 논문에선 1번에서 바로 3번이 유도될 수 있다고 언급하며, 2, 5, 6, 7번은 appendix 에 넣는다. 그래서 이 논문이 내겐 다 읽어도 찜찜했다. 증명은 본문에 아예 등장하지도 않기 때문이다.
• 우선 위 순서를 따라가며, 최대한 이해해보자.

 

A. 기호 및 수식 정의하기

• 여기까지는 매우 쉽다.

 

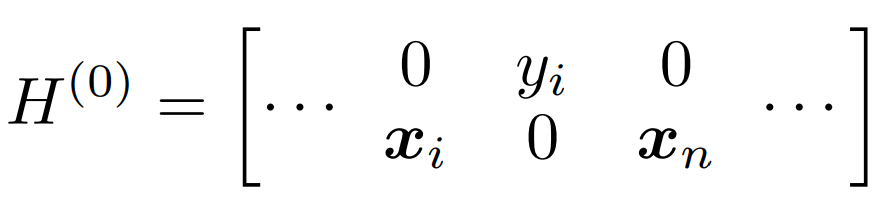
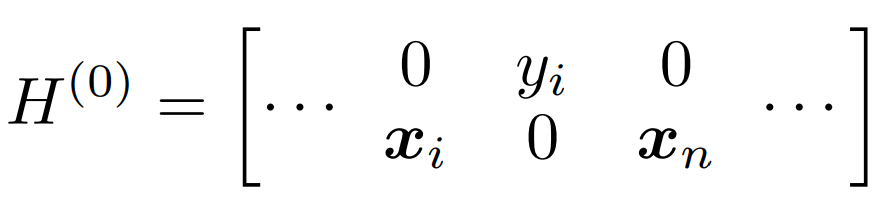
• 똑같은 그림을 왜 2장 넣었냐 하실 수 있는데, 의도했다.
• 아래쪽 행렬은 사실 (0) 이 아니라 (1) 이다. 이 숫자는 layer 층을 의미한다.
• 이 논문은 아래쪽으로 행렬이 늘어나는 형태로 층이 깊어진다는 전제를 당연히 깔고 있으나, 이 전제를 놓치면 매우 힘들다.
• 세로: 계층 깊이. 행은 d 단위로 늘어난다고 보시면 된다, 세로로 긴 벡터가 들어온다.
• 가로: 입력 순서. 문장에서 위치를 의미한다. 열은 1 단위이며 timestamp 라고 표현한다. 그래서 t 라는 표현이 자주 등장한다.
• 예컨대, '나는 네가 좋아' 에서 t = 0 일 때 '나는', t = 1 일 때 '네가', t = 2 일 때 '좋아' 라고 보면 된다. 당연히 tokenizer 가 저렇게 공백 단위로 자르지 않겠지만, t 가 입력에서 순서를 의미한다는 측면에서 비유한 것이다.

 

B. TRANSFORMER 수식 되짚기

: 안다, 벌써 읽기 싫다는 거. 근데 고수가 되려면, 이런 논문도 깊게 이해해봐야 한다. 가보자고. 혹시나 transformer 가 많이 헷갈리거나, 저 알고리즘을 제대로 공부한 적이 없다면 그걸 먼저 보는 걸 추천한다. 여기서 처음 이해하는 건 불가능에 가깝다.

 

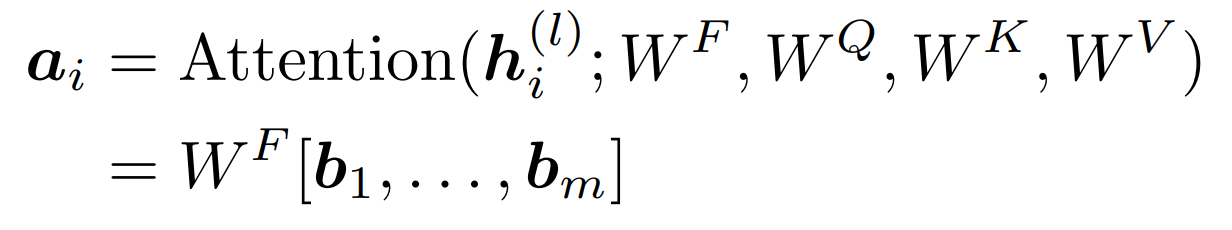
• ㅣ: 지금 layer 를 나타내는 숫자
• a: attention result
• i: index of sequence
• b: attention head
• j: index of attention head
• 혹시나 해서 말하자면,  여기서 WF는 multi head attention 결과를 합치기 위한 linear 이지, feed forward layer 에 등장하는 w matrix 가 아니다. 뒤에 나온다.
• 사견: 근데 왜 여기 수식엔 차원의 제곱근으로 나누는 게 포함되어 있지 않는거지? 생략할 거면, softmax 도 함께 하지 않나?

 

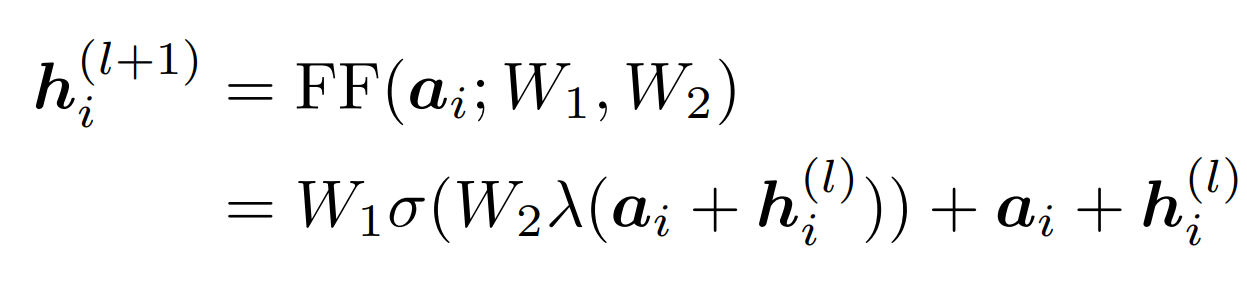
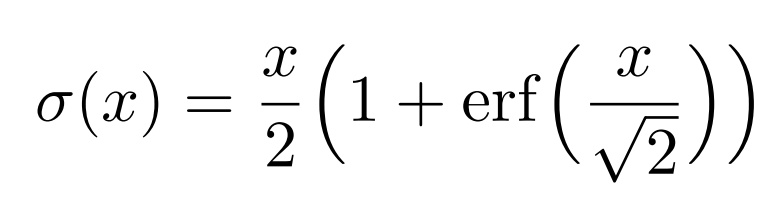
• 다음 layer 의 hidden states vector 를 구하기 위한 과정이다.
• add + norm: lambda 에서 하는 과정
• activation function 은 GELU 인데, 굳이 여기서 이해할 필요는 없다.
• NLP 를 공부한 사람이라면, 이렇게 다음 layer 의 hidden states vector 가 구해진다는 건 쉽게 받아들일 수 있을 것이다.

 

자, 위에서 봤던 식을 활용하면, 아래 4가지 연산이 가능하다는 걸 증명할 것이다. 논문에서는 이 과정을 appendix 로 빼놨다. 즉, self attention 이 아래 4가지 연산을 표현할 수 있다는 가정 하에 시작하는데, 나는 이 가정이 이해가 되지 않으니 이 논문을 읽는 내내 찜찜해서 처음으로 가져왔다.

 

C. RAW: Read-Arithmetic-Write operator

: attentition mechanism 이 요소 3번까지 표현가능하다는 걸 증명하기 위해, 2번 요소를 정의하는 중이다. 마치 한번에 서울에서 부산까지 운전하면 피곤하니 중간에 휴게소를 지었다는 비유로 이해해주길 바란다.

 

 

그렇다면, 그 중간 단계 역할을 할 식은 어떻게 세워졌을까?

 

ㄱ. Operators read some hidden units from the current or previous timestep

 

• 먼저, 읽는다는 연산이 들어가야 한다.
• transformer 알고리즘 특성상, 현재 상태나 과거 상태를 불러올 수 있어야 한다.
• 그래서 다음과 같이 수식을 먼저 설계했다고 한다.
• 일단, W, h, K 가 뭔지 알려고 하지 말고, 이건 읽는 연산이구나 정도만 받아들이자. 뒤에 이 식을 증명하는 과정에서 자연스럽게 알게 된다.
• 그래도 굳이 알고 싶다면, Wa 는 여기서 저자가 잘못 그린 것 같다. 뒤에서 나오는 최종 수식에는 Wa 가 분자에 등장한다.
• 그리고 h(l) 을 사용해서 h(l+1) 을 만들기 때문에, h(l) 언급되는 것만으로도 read 라고 간주하는 느낌이라고 보면 된다.

 

ㄴ. Operators perform element-wise arithmetic between the quantity read in step 1 and another set of entries from the current timestep

• 봐라, Read 연산 생김새가 달라졌다. 어차피 마지막에 수식을 자세히 이해해도 된다.
• 연산자는 현재 상태와 읽어온 값 사이에 element wise 연산이 있어야 한다고 말한다.
• 연산자는 크게 더하기와 곱하기가 있는데, 추후에 보면 별표로 두 연산 모두 지칭할 수 있도록 해둔다.
• 그냥 transformer 에 필요한 연산을 하나씩 추가해서 RAW 라는 연산자를 만들고 있구나 정도로만 받아들이자.

 

ㄷ. Operators reduce, then write to the current hidden state

• 마지막으로 계산 결과를 Wo 와 같은 linear 를 통해 reduction 할 필요가 있다
• 그런 연산을 마지막에 추가해주면, 다음 layer 의 hidden states vector 가 만들어진다고 볼 수 있다.
• 이렇게 3개를 반영해서 식을 만들어봤구나 정도로 이해하자.

 

ㄹ. RAW 정의하기

• 갑자기 수식말고 영어도 함께 등장하니 혼란스럽겠지만, 이제 제대로 정의하기 때문에 다 봐야 한다.
• 입력과 출력의 형태가 같고, 별표 연산은 더하기나 요소별 곱을 의미한다.
• K: a map from current timesteps to target timesteps 을 의미한다.
• r, s, w: 이건 리스트라고 보면 된다. 우리가 파이썬에서 h[1:10] 이렇게 표현하면, 1 ~ 9까지 값만 가져오는 것처럼 r, s, w 도 똑같다.
• 수식이 26, 27번이 있는데 w에 속하면 RAW 연산자를 거친 결과가 다음 레이어에 등장하는 것이고(26), w에 속하지 않으면 그냥 이전 레이어 값을 그대로 가져온다는 의미다(27).
• 당연히 이 정의만 보고 바로 이해하기 어렵다. 추후에 2번과 3번이 동치라는 6번 증명을 할 때, 명확히 이해가 될 것이다.

 

 

D. Single Transformer  Layer → RAW

• 하나의 트랜스포머 레이어로도 RAW 가 구현가능하다는 걸 증명할 것이다.
• 여기서 핵심은 하나의 레이어로도 충분하다는 점.
• 하지만 나는 설명하지 않는다. 아무리 부록을 쳐다봐도 도저히 이해가 어렵고, 그걸 넘기고 읽어도 말이 안 된다...궁금하신 분들은 18 ~ 25 페이지를 읽고 이해에 도전해보시길. 혹시나 이해한다면 저도 알려주세요!

 

E. 4가지 연산 이해하기

1. mov

 

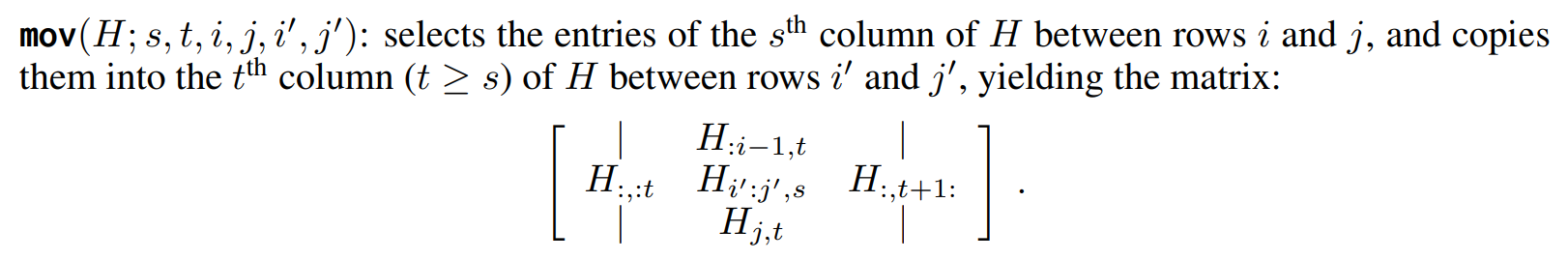
• 일단 직관적으로 move 니까, 's열에 있는  i:j 행'을 't열에 i':j'행'으로 복사한다는 의미라고 생각하면 된다.
• 그림이 조금 헷갈리지만, 가운데 H 3개가 있는 곳이 t 열이고, 정 가운데 있는 H가 복사되어 옮겨졌다고 보면 된다.

 

2. div

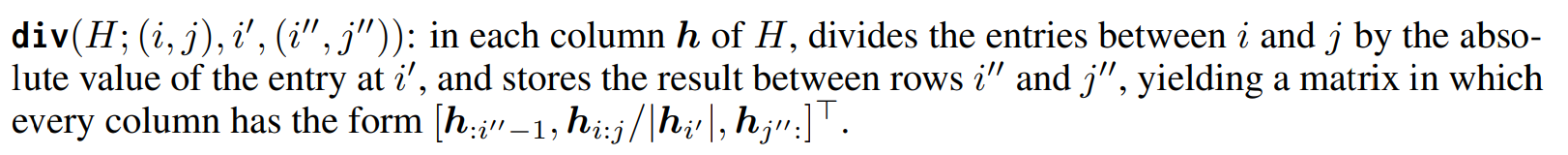
• 굉장히 쉽다. 읽기만 해도 한번에 이해가 된다. 단, column 별로 모두 진행한다는 것만 상기하자.

 

3. aff

• 이하동문으로 쉽다.

 

4. mul

• 사실 이게 2번인데, 4번으로 미룬 이유는 이해가 늦어져서다. 3번까지 이해했는데, 4번이 이해가 안 된다면, 논문 13페이지를 차근차근 읽어보면 분명 이해가 될 것이다.

 

F. RAW → mov, mul, aff, div

• 위에서 언급한 4가지 연산이 RAW 로 모두 표현가능하다는 걸 증명할 것이다
• 만약 이 증명이 성공한다면, Single Transformer Layer → RAW → mov, mul, aff, div 까지 이해한 셈이다.

 

• 당장 연필을 꺼내서 RAW에 대입해보면서 식을 정리하면 동치라는 걸 이해할 수 있다.
• 눈으로 이해하면, 이해가 잘 안 되니 mov 라도 꼭 직접 대입해보길 바란다. 그러면 K, w, r, s 가 뭔지 감이 잡힌다.

 

G. multiple mov, mul, aff, div → linear regression

• 이제 마지막 증명이다. 4가지 연산으로 linear regression 이 만들어진다는 걸 증명할 것이다.
• 그러면 이렇다. Single Transformer Layer → RAW → mov, mul, aff, div → linear regression 이다.
• 엄밀히 말하자면, tranformer layer 여러 개로 linear regression 을 흉내낼 수 있다가 맞다.

 

• 이것만 보고 와닿으면 신이다.
• 요약본으로서 참고하길 바란다.
• 그래서 하나씩 증명하는 과정을 아래에 두었으니 그 흐름을 잡아가길 바란다.

 

세부 증명

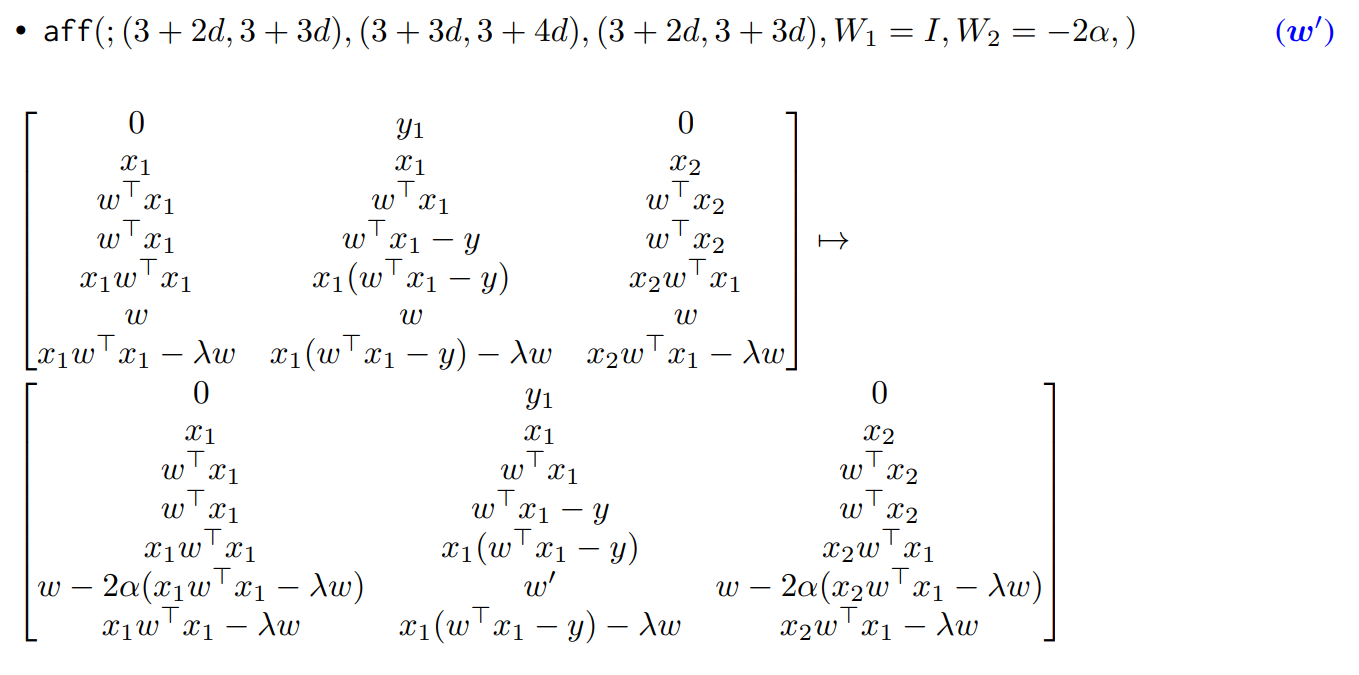
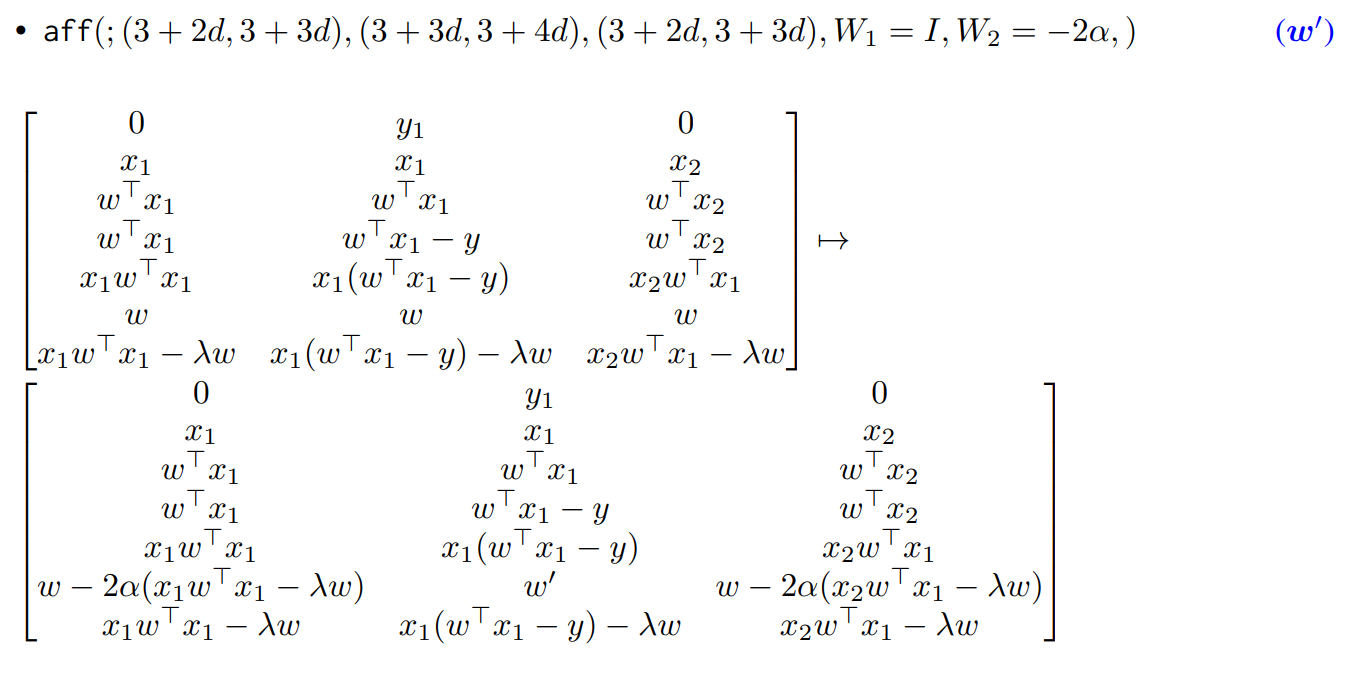
자, 여기까지 이해했다면 이제 논문의 요약을 다시 읽어보자.

 

H. Abstract

• 첫째, transformer 가 gradient descent 와 ridge regression 을 구현할 수 있음을 증명한다. (이건 위에서 내내 증명한 사실이다)
• 둘째, 실제로 'gradient descent, ridge regression, and exact least-squares regression 를 사용해 학습한 예측 모델'과 'in-context 모델'이 매우 근접하다는 것을 보일 것이다. 그리고 트랜스포머 깊이와 데이터 세트 노이즈가 변함에 따라 큰 폭과 깊이에 대해 베이지안 추정치로 수렴하는 것을 보여줄 것이다.
• 셋째,  in-context learner 가 레이어는 가중치 벡터와 모멘트 행렬을 비선형적으로 인코딩하여 위에서 언급한 알고리즘들의 특징을 갖고 있음을 직접적이진 않더라도, 어느 정도 증명합니다. (preliminary evidence 라는 표현을 직역하면, 예비 증명인데 확실한 증명은 아니지만 어느 정도의 증명이라는 뜻에서 의역했다.)
• 이러한 결과를 통해 in-context learning 을 어느 정도 알고리즘 측면에서 이해할 수 있다.

 

즉, 이제 실험을 통해 다른 알고리즘과 비교하며 얼마나 In context learning 이 유사한지를 비교해준다고 보면 된다. 눈치 빠른 분들은 아시겠지만, ridge regression 에 대한 증명은 넣지 않았다. 논문을 읽어보면 해주는데, 위에서 이해한 걸 토대로 충분하다고 생각하기 때문이다.

 

 

I. WHAT COMPUTATION DOES AN IN-CONTEXT LEARNER PERFORM?

: 논문 5페이지부터 시작한다

 

이 단원에서는 이런 이야기를 한다.

 

"transformer 로 block 단위로 구현을 통해, gradient descent 같은 알고리즘이 구현가능하다는 건 알겠어. 그런데 정말 train dataset 을 학습할 때, 저런 류의 알고리즘을 구현했을까? 아니면 아예 다른 알고리즘을 구현할 수 있잖아."

 

좋은 지적이다. 결국 내부적으로 무엇이 구현이 되어있는지 일일이 확인할 수 없다. 괜히 LM 을 black box 라고 부르겠는가. 다만, 실험적으로 어느 정도 검증이 가능하다. 예컨대, blackbox 1 과 black box 2 가 있다고 가정하자. 만약 똑같은 입력을 넣었을 때, 똑같은 결과가 출력된다면? 그리고 많은 입력에 대해서도 그렇다면? 그럴 땐, blackbox1 과 blackbox 2 는 동치라고 본다.

 

물론 해당 논문에선 아예 동일할 리가 없다. 그러므로 얼마나 유사한지를 측정하기 위한 metric 을 소개한다.

 

Squared prediction difference

• 복잡해보이지만, MSE 랑 똑닮았다.
• 차이를 구해서 제곱한다고 생각하자.

 

Implicit linear weight difference

• 결과 이외에도 내부적으로 weight 를 추정해서 구할 수는 없을까라는 생각으로 만들어진 지표다
• 알고리즘 A가 만약 linear function 이었다고 가정하고, 그 경우의 W 를 구해본다
• 그렇게 구해진 W 간의 차이를 평균(expectation)으로 구했다고 보면 된다
• 이를 통해, 단순히 결과 차이뿐만 아니라 내부적인 구현의 차이도 어느 정도 근사해서 접근했다고 볼 수 있다

 

실험 설정

• 여기에 표기되지 않은 상황은 input dimension = 8 이라는 점이다. gaussian 분포로 뽑을 때, 8차원 x 를 뽑아서 y 를 예측하는 것으로 보인다.

 

실험1: ICL matches ordinary least squares predictions on noiseless datasets

• KNN: 갑자기 나온 이유는 모르겠지만, 기존 데이터에서 새로 예측해야 할 데이터 기준 거리가 가장 가까운 3개의 y 값을 평균냈다고 한다.
• One-pass stochastic gradient descent: batch = 1 일 때, 주어진 예제를 모두 계산한 것
• One-step stochastic gradient descent: batch 단위로 한 번에, 주어진 예제를 모두 계산한 것
• Ridge regression: Ridge 형식으로 미분하는 방식으로 푼 것
• OLS: 정규화가 포함되지 않은 ridge regression
• 사견: 어떤 알고리즘과 가장 유사한지 보기 위해 다양한 경우를 생각해서 고안한 것을 보인다

 

• 아래 그림에 색깔이 무엇인지 적혀 있으니 참고할 것
• 녹색과 주황색 선이 예제 개수와 관계 없이 0 에 수렴하는 것을 볼 수 있다
• 즉, OLS 와 Ridge 형태가 가장 가깝다
• Gradient Descent 도 개수가 증가함에 따라 0 에 가까워짐을 볼 수 있다

 

• 개수가 10개를 넘자, W 에서도 차이를 거의 보이지 않는다
• 내부적으로도 In Context Learner 가 위 알고리즘들을 잘 따라가고 있음을 의미한다

 

결론적으로 깔끔한(noiseless) 데이터셋에선 잘 동작한다. 하지만 noise 가 추가된다면 어떨까? 이때의 실험 결과로 더욱 정확히 밝힐 수 있을 것이다.

 

실험2: ICL matches the minimum Bayes risk predictor on noisy datasets

• noise 역시 gaussian 으로 예측값에 더해졌으며, 아무리 많은 예제를 줘도 정확히 예측할 수 없게 되었다.

 

 

• 위는 bayesian estimator 인데, ridge regression 과 동일하게 생겼다
• 이 점을 이용하여, prior 와 noise 의 분산을 조절해가며 In Context Algorithm 이 어떻게 움직이는지 보기로 했다

 

• Ridge 와 SPD 를 구한 결과, ICL 은 분산을 조절하는 그대로 다 따라온다
• 가장 아래 적힌 숫자가 분산이고, 그 분산에 따라 ridge 안에 있는 숫자가 동일한 분포에서 가장 작은 차이를 보이기 때문이다
• 이를 통해 In Context Learning 이 Bayesian estimator 의 형태를 따른다고 볼 수 있다

 

실험3:  모델의 능력은 어디서 나오는 것일까?

• 위 두 실험은 계산능력이 충분히 큰 모델로 ICL이 진행되었기 때문에 문제가 없었다.
• 그렇다면, 모델을 축소시킨다면 성능이 달라질까?
• hidden size 나 depth 에 변화를 주며 실험했다

 

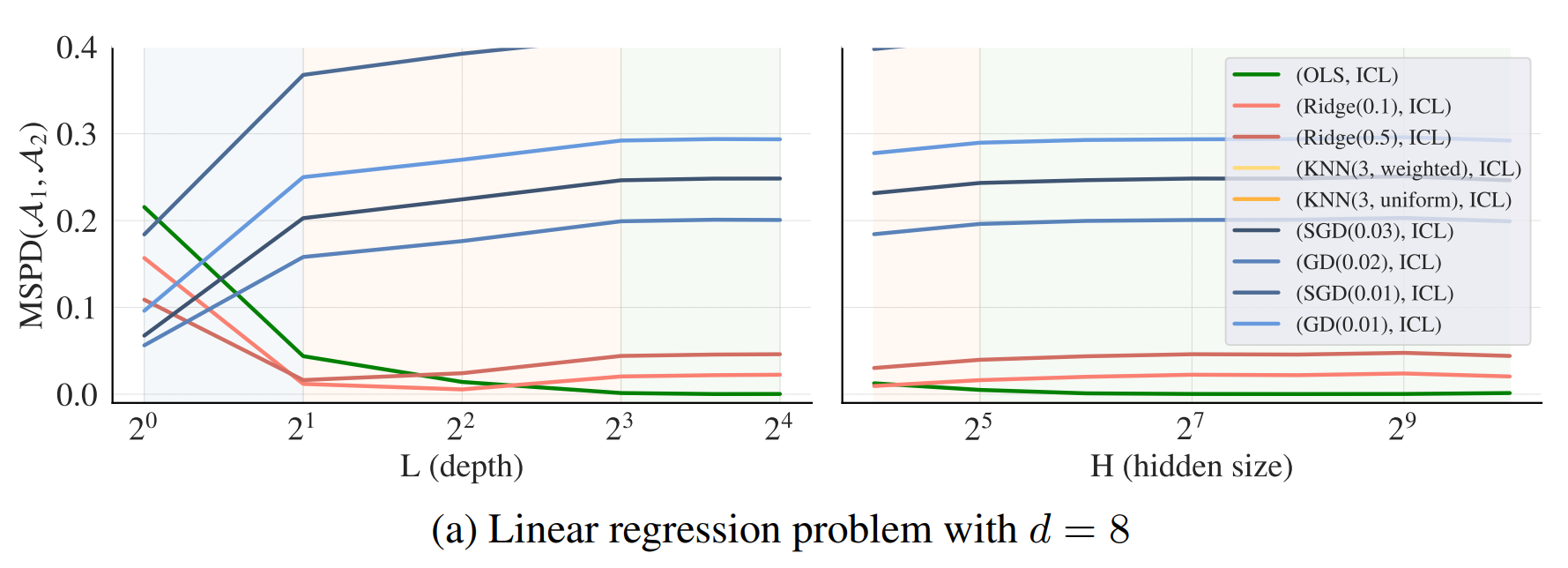
저자는 크게 3가지 특징을 보인다고 말한다.

 

depth: 깊이

• 가장 층이 얇을 때, gradient descent 와 유사하다
• 중간 층에서는 Ridge 와 가장 유사하다
• 깊은 층에서는 OLS 와 가장 유사해진다

 

hidden size

• 커질수록 ridge regression 과 유사하다
• ICL이 더욱 효과적인 알고리즘을 찾아간다고 해석할 수 있다

 

하지만 여기까지의 실험으로도 computation level 에서 standard learning algorithm 과 유사함을 보인 것이지, algorithm level 에서는 여전히 어떤 것도 밝히지 못했다.

 

실험4: 중간 중간 단계별로 어느 정도 확인할 수 있지 않을까?

• algorithm 을 파헤칠 수는 없어도, 중간 중간 단계별로 확인하여 어느 정두 유추할 수 있지 않을까?
• probe model 이라는 걸 정의해서 확인해보자.

 

probe model

• 수식이 probe 라는 모델이다
• 이 모델에 대해서 알아야 할 건 2가지다
• 1. 입력은 해당 중간 layer hidden states vector 이며, 출력은 최종 결과 y 다
• 2. FF 라는 기호가 있는데, 이걸 linear 나 MLP 로 넣어서 실험했다

 

그렇다면, 이걸로 대체 뭘 알아낼 수 있다는 것인가? 예를 들어, layer 7 에서 나온 hidden states vector 로 결과를 예측하도록 probe model 을 학습했다고 가정하자. 그리고 이때, FF = linear 라고도 해주자. 만약 이렇게 학습한 모델이 여전히 error 값이 크다면, 적어도 'layer 7 과 result 사이에 구현된 알고리즘은 non linear 할 가능성이 높구나' 하고 추측해볼 수 있다.

 

• 위 결과를 보면, 모든 지표에서 linear 가 MLP 보다 차이가 크다는 걸 알 수 있다
• 그래서 ICL 이 구현하는 알고리즘은 non linear 할 가능성이 높다고 이야기한다
• 사실 이 실험에 대한 결과가 하나 더 있긴 한데, 워낙 내게는 어려워서 여기까지밖에 해석할 수 없다...미안하다

 

결론

• ICL 의 원리를 파헤치는 다양한 실험 결과를 제공했다
• 우리는 multiple linear regression algorithm 을 transformer 가 구현할 수 있음을 수식적으로/실험적으로 보였고, 중간 단계에서도 확인할 수 있었다
• 우리 실험은 linear 에 초점을 맞췄지만, 추후 실험들은 다양하게 나아갈 수 있으며 그 첫 발을 우리가 내딛었길 바란다

 

의견

• 가능성을 수식적으로 보인 것만으로도 대단하다고 생각함. 이런 발상을 끝까지 실험했고, 그 방식이 다양하며 합리적이라서 배울 점이 많았다고 생각함.
• 다만, 학회에 제출해야 해서 그런가 appendix 로 많은 내용이 빠지는 바람에 논문만으로 깔끔하게 이해할 수 없게 됨. 실험 자체가 워낙 치밀하고 설계 및 증명 과정이 많기 때문에 가독성 부분에서는 매우 낮은 점수를 받을 수 밖에 없는 논문임.
• 영어권 사람이 아니라서 그런지 몰라도, 여태 읽었던 논문에 비해 난이도가 굉장히 높았으며 아직도 이해되지 않는 부분들이 많음. 개인적으로 이 정도는 알겠지하고 생략되거나 설명하지 않은 부분들이 꽤 있는데, 그게 NLP 연구자들조차도 언급하지 않으면 힘들 수 있겠단 생각이 들었음.
• transformer 가 이런 알고리즘을 구현할 수도 있다에 가까운 것이지, 실제로 이렇게 매번 바꿔가며 구현하고 있다를 확실히 증명한 것은 아님. linear regression 에 집중한 논문이라, 실제로 자연어 예제가 포함된 In Context Learning 에서는 어떤 양상을 띄는지 알 수 없긴 함.