이 글을 이해하려면, RLHF에 대한 이해가 필요하니 아래 블로그부터 읽으면 좋다.
https://heygeronimo.tistory.com/122
[논문이해] training language models to follow instructions with human feedback
논문을 이해하고 싶다면 아래 글을 읽으세요. 너무 잘 써서 이것보다 더 잘 쓸 자신이 없어요. https://taeyuplab.tistory.com/10 [논문 리뷰] InstructGPT: Training language models to follow instructions with human feedback
heygeronimo.tistory.com
이 글의 관심사는 오로지 수학적인 유도 과정이다. 나처럼 인공지능을 머신러닝이나 수학적 기초 없이 들어온 MZ연구자들은 ELBO나 깁스 부등식 등 수학적인 유도가 긴 논문을 기피하게 된다. 나 역시 그럴 때가 많아 일부러 몇몇 논문들은 수학적 증명으로 가득 찬 논문을 정리하기도 했다.
DPO가 등장한지 꽤 오래되었는데도, 최근 언어모델에서도 계속 사용하는 추세인 것 같아 손실함수 유도과정을 살펴보았다.
RLHF에서 DPO로 넘어갈 땐 reward model 이 사라졌다는 점을 명심하자
: 즉 유도 과정의 핵심은 보상 모델의 학습 없이 손실 함수를 구성하는 것

- r은 최대화하면서도 기존 언어 모델의 분포를 유지하도록 만든 식이다

- KL-divergence 식을 전개했다.
- 이때, y에 관한 Expectation을 분리했고 그 안에 KL-divergence 를 집어넣었기 때문에 π(y|x)가 사라졌다
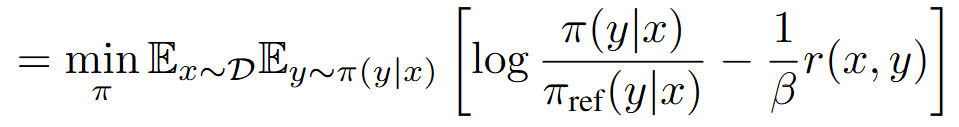
- 모든 항에 '- 1 / β '를 곱한다
- 그래서 max 가 min 으로 변했다

- 여기서 갑자기 급발진하는 것처럼 보인다. 하지만 침착하게 살펴보자.
- z(x)는 어떻게 생겼든 전개해보면 사라지는 항이다. 그냥 사라지는 항을 추가했다고 보자.
- 나머지 항들은 log 안에 쑤셔넣으면 저 모양이 된다.
- 왜 이런 짓을 하는지 일단 이해하지는 말고, 어쨌든 전개하면 똑같으니까 이 정도만 이해하자.

- z(x)는 어떻게 생겼든 전개하면 날아간다고 여러 번 말했다
- 즉 반대로 말하면, 내 마음대로 정의해도 된다
- 그러니까 위 식처럼 생겼다고 가정해보자

- 이건 뭐냐고? 이것도 마음대로 정의한거다.
- ' π*(y|x) '라는 식을 만들어봤다
- 단, z(x)가 분배함수인 형태로 만들어봤다
- 정의는 마음대로니까 이해할 필요 없고, 그냥 이렇게 위 식 2개를 정의했구나 하고 받아들이면 된다.
- 이때 ' π* (y|x) '는 ' π(y|x)'와 무관한 식이라는 것만 기억하면 된다.

- 이제 위에서 정의한 π와 π*을 기존 식에 대입하고 정리하면 위와 같아진다
- 자, 지금부터 중요하다
- 우선 z(x)는 π와 관련 없는 식이니까 위 식을 최소화하는데 아무런 영향을 주지 못하므로 무시해도 된다
- 그렇다면, KL-Divergence 항을 최소화하는 것이 핵심이다
- 이때 깁스 부등식을 활용한다. 깁스 부등식이 뭔지 잘 몰라도 된다. 확실한 것은 깁스 부등식에 의해, KL-Divergence 항이 가장 작아지는 하한선이 이미 있다는 점만 기억하면 된다.

- 그 하한선의 조건은 바로 P = Q, 즉 서로 다른 분포의 차이가 가장 작을 때는 당연히 두 분포가 같을 때다
- 여기서 P와 Q는 π*와 π이므로 이 둘이 같을 때 위 식을 최소화할 수 있다
- 그래서 진짜로 두 항이 같다고 적어놓은 것이고, 그 결과 전개하면 위와 같은 셈
근데 우리의 목적이 뭐였겠는가, 당연히 r(x, y)를 구하지 않는 것이다.
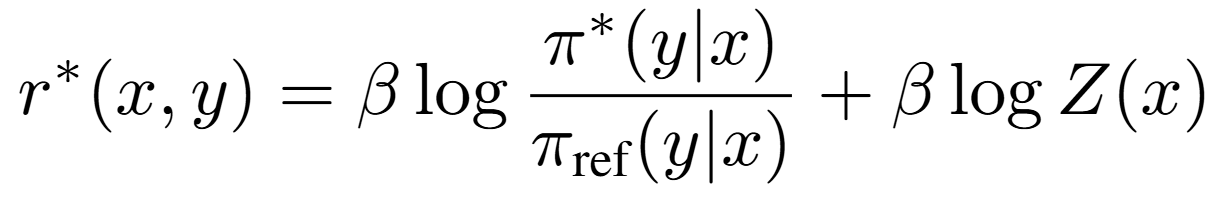
- 그래서 r(x,y)에 관해 정리하면 위 식처럼 표현이 가능하고 이게 최적의 보상 함수라고 가정한다
- 이게 DPO로 보상 모델을 따로 학습하지 않고, 수식으로 전개해서 최적의 보상 함수를 찾은 것이다
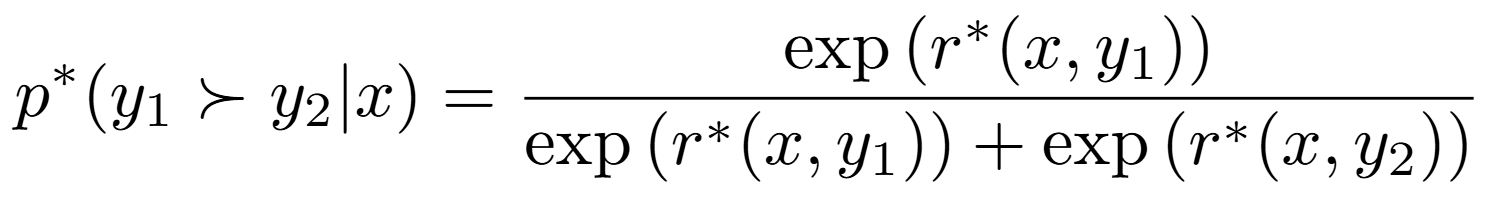
- 자, 원래 이 식부터 출발했는데 r(x,y)를 알고 있으니 대입해보자
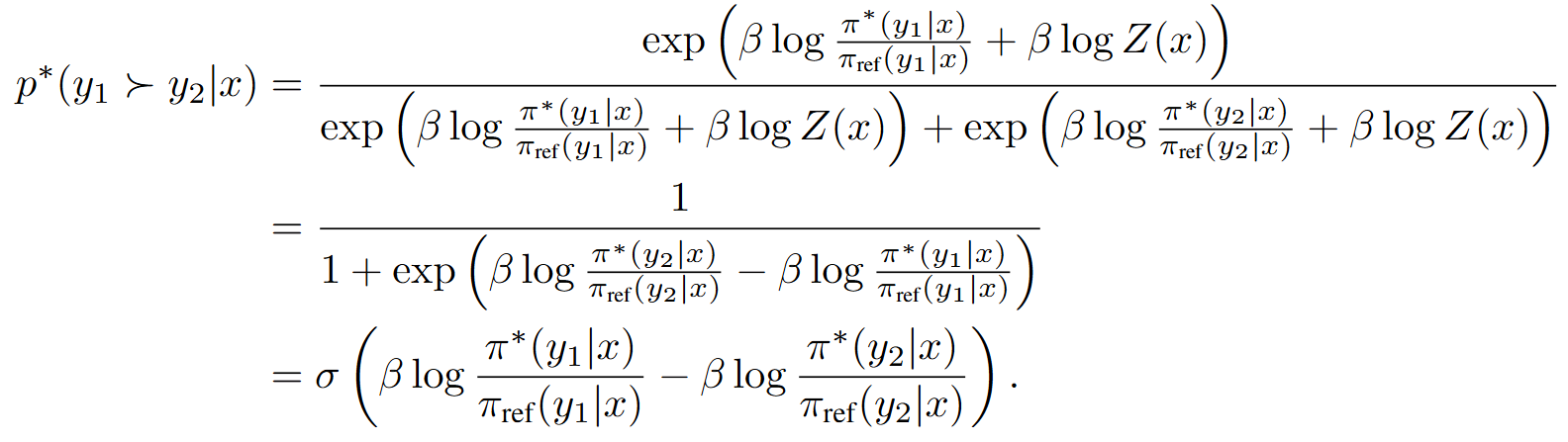
- 대입한 결과, DPO에서 정의한 손실함수가 도출되었음을 알 수 있다



